m:n = \(2\frac{1}{3} : 1\frac{1}{5}\) and n : q = \(1\frac{1}{2} : 1\frac{1}{3}\), find q : m.
- A. 35 : 18
- B. 16 : 35
- C. 18 : 35
- D. 35 : 16
The radius of a sphere is 3 cm. Find, in terms of π, its volume.
- A. \(30\pi cm^3\)
- B. \(108\pi cm^3\)
- C. \(27\pi cm^3\)
- D. \(36\pi cm^3\)
Find the value of a in the equation: cos (a + 14)° = sin (4a + 6)°
- A. 15
- B. 17
- C. 14
- D. 21
The radius and height of a solid cylinder is 8 cm and 14 cm respectively. Find, correct to two d.p the total surface area.
(Take \(\pi = \frac{22}{7})\)
- A. \(1,106.29cm^2\)
- B. \(1,016.29cm^2\)
- C. \(1,106.89cm^2\)
- D. \(1,206.27cm^2\)
A student measured the height of a pole as 5.98 m which is less than the actual height. If the percentage error is 5%, find correct to two d.p the actual height of the pole.
- A. 6.29m
- B. 7.67m
- C. 7.18m
- D. 6.65m
Find the roots of the equations: \(3m^2 – 2m – 65 = 0\)
- A. \(( -5, \frac{-13}{3})\)
- B. \(( 5, \frac{-13}{3})\)
- C. \(( 5, \frac{13}{3})\)
- D. \(( -5, \frac{13}{3})\)
If \(log_a 3\) = m and \(log_a 5\) = p, find \(log_a 75\)
- A. \(m^2 + p \)
- B. 2m + p
- C. m + 2p
- D. \(m + p^2\)
Solve \(2^{5x} \div 2^x = \sqrt[5]{2^{10}}\)
- A. \(\frac{3}{2}\)
- B. \(\frac{1}{2}\)
- C. \(\frac{1}{3}\)
- D. \(\frac{5}{3}\)
The interior angle of a regular polygon is 6 times its exterior angle find the number of sides of the polygon.
- A. 12
- B. 15
- C. 10
- D. 14
Evaluate, correct to three decimal place \(\frac{4.314 × 0.000056}{0.0067}\)
- A. 0.037
- B. 0.004
- C. 0.361
- D. 0.036
Express \(413_7\) to base 5
- A. \(2311_5\)
- B. \(1131_5\)
- C. \(1311_5\)
- D. \(2132_5\)
For what value of x is \(\frac{ x^2 + 2 }{ 10x^2 – 13x – 3}\) is undefined?.
- A. \(\frac{1}{5}, \frac{3}{2}\)
- B. \(\frac{-1}{5}, \frac{3}{2}\)
- C. \(\frac{1}{5}, \frac{-3}{2}\)
- D. \(\frac{-1}{5}, \frac{-3}{2}\)
Simplify \(3\sqrt{12} + 10\sqrt{3} – \frac{6}{\sqrt{3}}\)
- A. 10\(\sqrt{3}\)
- B. 18\(\sqrt{3}\)
- C. 14\(\sqrt{3}\)
- D. 7\(\sqrt{3}\)
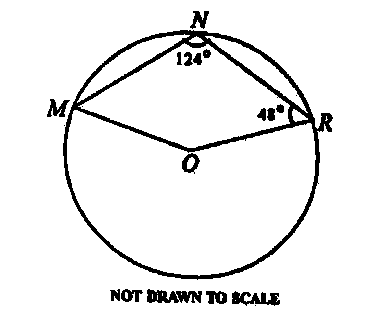
In the diagram above, M, N, R are points on the circle centre O. ∠ORN = 48° and ∠RNM = 124°. Find ∠OMN.
- A. \(58^0\)
- B. \(64^0\)
- C. \(48^0\)
- D. \(76^0\)
One-third of the sum of two numbers is 12, twice their difference is 12. Find the numbers.
- A. 22 and 14
- B. 20 and 16
- C. 21 and 15
- D. 23 and 13
The angle of elevation of the top of a building from a point Z on the ground is 50°. If the height of the building is 124 m, find the distance from Z to the foot of the building.
- A. 147.78m
- B. 104.05m
- C. 161.87m
- D. 192.91m
Mr Manu is 4 times as old as his son, Adu. 7 years ago the sum of their ages was 76. How old is Adu?
- A. 22years
- B. 12years
- C. 18years
- D. 15 years
There are 30 students in a class. 15 study woodwork and 13 study metal work. 6 study neither of the 2 subjects. How many student study woodwork but not metal work?
- A. 13
- B. 11
- C. 5
- D. 9
The angle of a sector of a circle of radius 3.4 cm is 115°. Find the area of the sector.
\((Take \pi = \frac{22}{7})\)
- A. \(11.6cm^2\)
- B. \(12.7cm^2\)
- C. \(10.2cm^2\)
- D. \(9.4cm^2\)
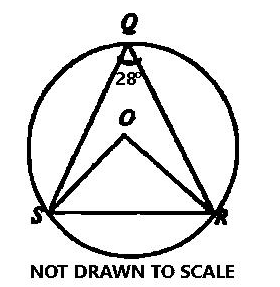
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
- A. \(56^0\)
- B. \(28^0\)
- C. \(76^0\)
- D. \(62^0\)


