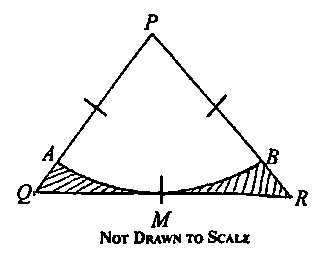
a. In the diagram above, PQR is an equilateral triangle of side 18 cm. M is the midpoint of QR. An arc of a circle with center P touches QR at M and meets PQ at A and PR at B. Calculate, correct to two decimal places, the area of the shaded region. (take \(\pi = \frac{22}{7})\)
Explanation
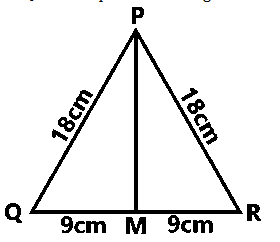
∆PQR is an equilateral triangle and M is the midpoint of Line QR. Hence, PM is the radius of the circle likewise Line PA and Line PB
Using Pythagoras theorem to find Line PM :
\( 18^2 = PM^2 + 9^2\)
\( PM^2 = 324 - 81 = 243\)
PM = \(\sqrt{243} = 9\sqrt{3}\)
∠QPR = \(\frac{180^0}{3} = 60^0\) ( each ∠ of an equilateral △ are equal)
Area of △,PQR = \(\frac{1}{2}absinθ\), but θ = 60°
= \(\frac{1}{2}\times18\times18sin60 = 81\sqrt{3} = 140.30 cm^2\)
Area of PAB = \(\frac{θ}{360} \times\pi r^2\)
= \(\frac{60}{360}\times \frac{22}{7} \times(9\sqrt{3})^2\)
= \(\frac{1}{6} \times \frac{22}{7} \times243\) = \(127.29cm^2\)
therefore, the Area of the shaded portion = area of △ PQR - area of sector PAB
= 140. 30 - 127.29 = \(13.01cm^2\) (to 2 d.p)

