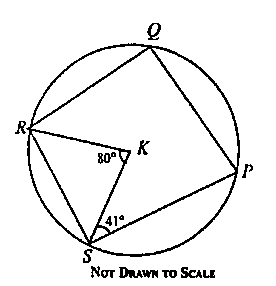
a. In the diagram above, P, Q, R, and S are points on the circle with centre K. KR is a bisector of angle ∠SRQ, ∠KSP = 41°, and ∠SKR = 80°. Find:
∠RQP;
b. Find ∠SPQ
Explanation
a. Since K is the centre and KR and KS are radii, ∆SKR is isosceles.
∠SRK + ∠RSK + ∠SKR = 180° (sum of angles in a triangle is 180o)
⇒ ∠SRK + ∠RSK + 80° = 180°
⇒ ∠SRK + ∠RSK = 180° - 80° = 100°
Since ∠SRK = ∠RSK (base angles of an isosceles triangle are equal)
∠SRK = ∠RSK = \(\frac{100^0}{2} = 50^0\)
∠RSP = 50° + 41° = 91°
∴ ∠ RQP = 180° - 91° = 89° (opp. angles of a cyclic. quad. are supplementary)
b. Since KR is a bisector of angle ∠SRQ:
∠SRK = ∠KRQ = 50°
∠SRQ = 50° + 50° = 100°
∴ ∠SPQ = 180° - 100° = 80° (opp. angles of a cyclic. quad. are supplementary)

