a. Copy and complete the tables of values of y = \(2x^2 – x – 4\) for -3 ≤ x ≤ 3
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 17 | -4 |
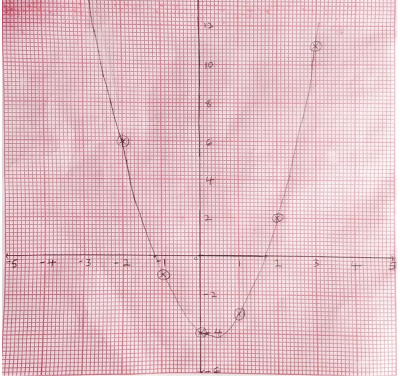
b. Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 unit on the y-axis, draw the graph of y = \(2x^2 – x – 4\) for -3 ≤ x ≤ 3.
ci. Use the graph to find: the roots of the equation \(2x^2 – x – 4\)
ii. Use the graph to find the: values of x for which y increases as x increases;
iii. Use the graph to find the: minimum point of y.
Explanation
a.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(2x^2\) | 18 | 8 | 2 | 0 | 2 | 8 | -18 |
| - x | 3 | 2 | 1 | 0 | - 1 | - 2 | - 3 |
| - 4 | - 4 | - 4 | - 4 | -4 | -4 | -4 | -4 |
| y | 17 | 6 | -1 | -4 | -3 | 2 | 11 |
b. the graph above, solution to question 8b.
ci. The roots of the equation from the graph are -1.2 and 1.7.
ii. Let y = \(2x^2 - x - 4\)
\(\frac{dy}{dx}\) = 4x - 1
At critical point \(\frac{dy}{dx}\) = 0
so that 4x - 1 = 0;
x = \(\frac{1}{4}\)
Using test points:
1. we use a test point less than \(\frac{1}{4}\), e.g x = 0
\(\frac{dy}{dx}\)(0) = 4(0) - 1 = -1
at this point, y = \(2x^2 - x - 4\) is decreasing
2. we use a test point greater than \(\frac{1}{4}\) e.g x = 1
\(\frac{dy}{dx}\)(1) = 4(1) - 1 = 4 - 1 = 3.
at this point, y = \(2x^2 - x - 4\) is increasing.
so, the function y = \(2x^2 - x - 4\) increases as x increases when x is greater than \(\frac{1}{4}\)
Therefore, the value of x for which y increases are x is greater than \(\frac{1}{4}\)
iii. The minimum point of y = -4.1.

