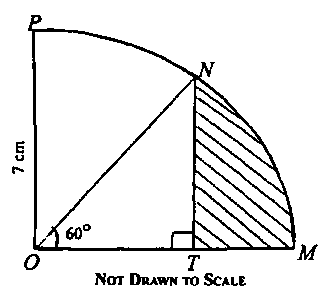
a. In the diagram above, the radius of the sector of circle centre O is 7 cm and ∠MON is 60°. Find, correct to one decimal place, the area of the shaded portion. (take \(\pi = \frac{22}{7})\)
b. The x and y intercepts of a straight line are \(\frac{-3}{4} and \frac{2}{7}\) respectively. Find the equation of the line.
Explanation
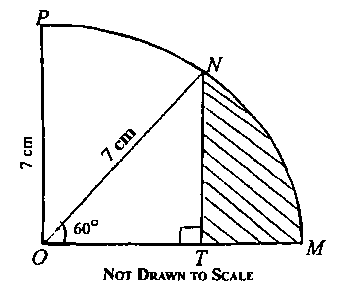
a. Area of sector MON = \(\frac{MON}{360} \times\pi r^2\)
= \(\frac{60}{360}\times\frac{22}{7}\times7^2\)
= \(\frac{77}{3}cm^2\)
\(\frac{NT}{7}\) = sin60°
NT = 7sin60° = \(7\times\frac{\sqrt{3}}{2}\) = \(7\times\frac{\sqrt{3}}{2}\)cm.
\(\frac{OT}{9} = cos60^0\)
OT = 7cos60° = \(7\frac{1}{2}\)cm
Area of △ONT = \(\frac{1}{2}\times OT\times NT\)
= \(\frac{1}{2}\times\frac{7}{2}\times\frac{7\sqrt{3}}{2} = 49\sqrt{3}{8}cm^2\)
Area of shaded portion = Area of sector MON - Area of △ONT
= \(\frac{77}{3} - \frac{49\sqrt{3}}{8}\) = 25.67 - 10.61 = \(15.06cm^2\) = 15.1\(cm^2\)
b. Given : y = mx + c; hence ; x = \(\frac{ y - c }{ m } = \frac{ y }{ m } - \frac{ c }{ m }\)
x-intercept = \(\frac{ - c }{ m } = \frac{ - 3 }{ 4 }\)
Therefore, m = \(\frac{4}{3}\)c ....................... (1)
But y-intercept, c = \(\frac{2}{7}\)
Therefore, m = \(\frac{4}{3}\times\frac{2}{7} = \frac{8}{21}\)
Equation of straight: y = mx + c
y = \(\frac{8}{21}x + \frac{2}{7}\) OR 21y = 8x + 6 = 8x - 21y = - 6

