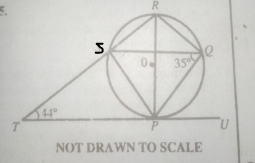
In the diagram \(\overline{TU}\) is a tangent to the circle SPQR at P. If \(\angle\)PTS = 44º, \(\angle\)SQP = 35º, find \(\angle\)PST
-
101º
- 125º
- 130º
- 135º
The correct answer is: A
Explanation
\(\angle\)SPT = 35º (alternate segment)
From \(\triangle\)TSP
44 + \(\angle\)SPT + \(\angle\)PST = 180º (sum of angles in a triangle)
\(\angle\)PST = 180 - 44 - 35 = 101º