A die is tossed once. Find the probability of getting a prime number.
- A. \(\frac{1}{2}\)
- B. \(\frac{1}{6}\)
- C. \(\frac{1}{3}\)
- D. \(\frac{2}{3}\)
Two opposite sides of a rectangle are (5x + 3) m and (2x + 9) m. If an adjacent side is (6x – 7) m, find in m\(^2\), the area of the rectangle.
- A. 45
- B. 65
- C. 125
- D. 165
The following are the masses (in kg) of members in a club: 59, 44, 53, 49, 57, 40, 48, and 50. Calculate the variance of the distribution.
- A. 35
- B. 36
- C. 40
- D. 50
The following are the masses (in kg) of members in a club: 59, 44, 53, 49, 57, 40, 48, and 50. Calculate the mean mass.
- A. 44 kg
- B. 50 kg
- C. 40 kg
- D. 53 kg
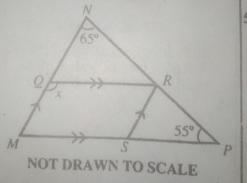
Find the value of x in the diagram above.
- A. 120º
- B. 100º
- C. 60º
- D. 150º
Four of the angles of a hexagon sum up to 420º. If the remaining angles are equal, find the value of each of the angles.
- A. 60\(^O\)
- B. 100\(^O\)
- C. 120\(^O\)
- D. 150\(^O\)
The perimeter of a rectangular garden is 90 m. If the width is 7 m less than the length, find the length of the garden.
- A. 19 m
- B. 23 m
- C. 24 m
- D. 26 m
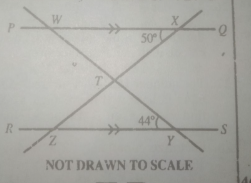
In the diagram above, \(\overline{PQ}\) || \(\overline{RS}\), \(\angle\)WYZ = 44º and \(\angle\)WXY = 50º. Find \(\angle\)WTX
- A. 65º
- B. 68º
- C. 86º
- D. 90º
The gradient of the line joining the points P(2, -8) and Q(1, y) is -4. Find the value of y
- A. 2
- B. 4
- C. -4
- D. -3
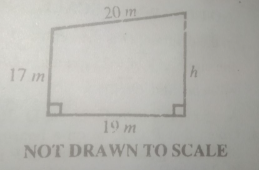
Find, correct to the nearest whole number, the value of h in the diagram above.
- A. 15 m
- B. 22 m
- C. 23 m
- D. 18 m
A cone and a cylinder are of equal volume. The base radius of the cone is twice the radius of the cylinder. What is the ratio of the height of the cylinder to that of the cone?
- A. 5: 4
- B. 4: 3
- C. 3: 2
- D. 3: 4
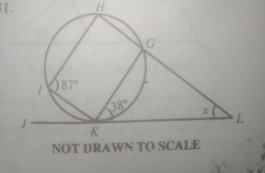
In the diagram above, JKL is a tangent to the circle GHIK at K.
- A. 93º
- B. 55º
- C. 42º
- D. 23º
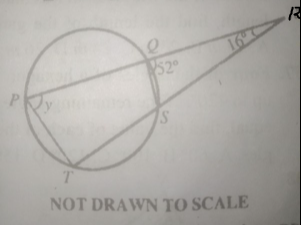
In the diagram above, < SQR = 52º and < PRT = 16º. Find the value of the angle marked y
- A. 64\(^0\)
- B. 68\(^0\)
- C. 112\(^0\)
- D. 128\(^0\)
For what values of x is \(\frac{x – 3}{4}\) + \(\frac{x + 1}{8}\) \(\geq\) 2 ?
- A. x \(\geq\) 5
- B. x \(\geq\) 6
- C. x \(\geq\) 7
- D. x \(\geq\) 8
Factorize completely: 27x\(^2\) – 48y\(^2\)
- A. 3(3x + 4y)(3x - 4y)
- B. 3(3x + 4y)(3x + 4y)
- C. 3(9x - 16y)(9x + 16y)
- D. 3(9x - 16y)(9x - 16y)
The number 1621 was subtracted from 6244 in base x. If the result was 4323, find x.
- A. Seven
- B. Eight
- C. Nine
- D. Ten
The length and breadth of a cuboid are 15 cm and 8 cm respectively. If the volume of the cuboid is 1560 cm\(^3\), calculate the total surface area.
- A. 976cm\(^2\)
- B. 838cm\(^2\)
- C. 792cm\(^2\)
- D. 746cm\(^2\)
Given that P is 25 m on a bearing of 330º from Q, how far south of P is Q?
- A. 25.2 m
- B. 21.7 m
- C. 19.8 m
- D. 18.5 m
A car valued at $ 600,000.00 depreciates by 10% each year. What will be the value of the car at the end of two years?
- A. $ 120,000.00
- B. $ 480,000.00
- C. $ 486,000.00
- D. $ 540,000.00
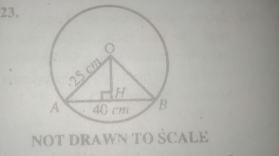
In the diagram above, O is the centre of the circle. If | \(\overline{OA}\) = 25 cm and |\(\overline{AB}\) = 40 cm, find |\(\overline{OH}\)|
- A. 15 cm
- B. 20 cm
- C. 25 cm
- D. 30 cm
A ladder 15 m long leans against a vertical pole, making an angle of 72º with the horizontal. Calculate, correct to one decimal place, the distance between the foot of the ladder and the pole.
- A. 15.8 m
- B. 14.3 m
- C. 4.9 m
- D. 4.6 m


