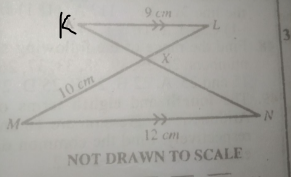
In the diagram above, \(\overline{MN} || \overline{KL}\), \(\overline{ML}\) and \(\overline{KN}\) intersect at X. |\(\overline{MN}\)| = 12cm, |\(\overline{MX}\)| = 10cm and |\(\overline{MN}\)| = 9cm. If the area of \(\triangle\) MXN is 16cm\(^2\), calculate the area of \(\triangle\) LXK
- A. 9cm\(^2\)
- B. 8cm\(^2\)
- C. 10cm\(^2\)
- D. 12cm\(^2\)
A piece of rod of length 44 m is cut to form a rectangular shape such that the ratio of the length to the breadth is 7: 4. Find the breath.
- A. 8m
- B. 14m
- C. 16m
- D. 24m
Find the quadratic equation whose roots are \(\frac{2}{3}\) and – 1
- A. 3x\(^2\) - x - 2 = 0
- B. 3x\(^2\) + x + 2 = 0
- C. 3x\(^2\) + x - 2 = 0
- D. 3x\(^2\) + x - 1 = 0
Gifty, Justina, and Frank shared 60 oranges in the ratio 5: 3: 7 respectively. How many oranges did Justina receive?
- A. 16
- B. 12
- C. 20
- D. 28
A number is added to both the numerator and the denominator of the fraction \(\frac{1}{8}\) if the result is \(\frac{1}{2}\), find the number.
- A. 3
- B. 4
- C. 5
- D. 6
Consider the following statements:
m = Edna is respectful
n = Edna is brilliant,
If m ⇒ n, which of the following is valid?
- A. ¬n ⇒ ¬m.
- B. ¬m ⇒ ¬n.
- C. n ⇒ ¬m.
- D. m ⇒ n.
Make R the subject of the relation V = πl(R\(^2\) – r\(^2\))
- A. R = \(\sqrt{\frac{V}{πl} + r^2}\)
- B. R = \(\sqrt{\frac{V}{πl} - r^2}\)
- C. R = \(\sqrt{V - πlr^2}\)
- D. R = \(\sqrt{V + πlr^2}\)
A cylindrical metallic barrel of height 2.5m and radius 0.245 is closed at one end. Find, correct to one decimal place, the total surface area of the barrel (Take π = \(\frac{22}{7}\))
- A. 2.1 m\(^2\)
- B. 3.5 m\(^2\)
- C. 4.0 m\(^2\)
- D. 9.4 m\(^2\)
A variable W varies partly as M and Partly inversely as P. Which of the following correctly represents the relation with k\(_1\) and k\(_2\) constants?
- A. W = \(\frac{k_1M}{k_2P}\)
- B. W = (\(k_1 + k_2\))\(\frac{\text{M}}{\text{P}}\)
- C. W = k\(_1\)M + \(\frac{k_2}{P}\)
- D. W = (k\(_1 + k_2\))M + P
If 3x – 2y = – 5 and x + 2y = 9, find the value of \(\frac{x – y}{x + y}\)
- A. \(\frac{5}{3}\)
- B. \(\frac{3}{5}\)
- C. \(\frac{-3}{5}\)
- D. \(\frac{-5}{3}\)
The interior angle of a regular polygon is 168º. Find the number of sides of the polygon.
- A. 24
- B. 30
- C. 15
- D. 12
A trader gave a change of # 540.00 instead of # 570.00 to a customer. Caculate the percentage error.
- A. 5\(\frac{5}{19}\)%
- B. 5\(\frac{5}{9}\)%
- C. 5\(\frac{7}{19}\)%
- D. 5\(\frac{7}{9}\)%
The population of a town increases by 3% every year. In the year 2000, the population was 3000. Find the population in the year 2003.
- A. 3,182
- B. 3,278
- C. 6,591
- D. 7,515
If log\(_3^{2x – 1}\) = 5, find the value of x
- A. 8
- B. 16
- C. 64
- D. 122
Find the sum for which $ 1,250.00 will amount to $ 2,031.25 at 12.5% per annum simple interest.
- A. 2 years
- B. 3 years
- C. 4 years
- D. 5 years
If (3 – 4\(\sqrt{2}\))(1 + 3\(\sqrt{2}\)) = a + b\(\sqrt{2}\), find the value of b
- A. -5
- B. 5
- C. -21
- D. 21
Simplify: (2p – q)\(^2\) – (p + q)\(^2\)
- A. 3p(p - 2q)
- B. 2p(p - 3q)
- C. 3p(2p - q)
- D. 2p(3p - q)
Express in index form: log\(_a^x\) + log\(_a^y\) = 3
- A. x + y = 3
- B. xy = 3
- C. xy = a\(^3\)
- D. x + y = a\(^3\)
The first term of an Arithmetic Progression (A.P) is 2 and the last term is 29. If the common difference is 3, how many terms are in the A.P.?
- A. 8
- B. 9
- C. 10
- D. 11
Given that P = {p: 1< p < 20}, where p is an integer and R = {r : 0 \(\leq\) r \(\leq\) 25, where r is a multiple of 4}. Find P ∩ R
- A. {4, 8, 10, 16}
- B. {4, 8, 12, 16}
- C. {4, 8, 12, 16, 20}
- D. {4, 8, 12, 16, 20, 24}
Multiply 3.4 x 10\(^{-5}\) by 7.1 x 10\(^8\) and leave the answer in standard form.
- A. 2.414 x 10\(^2\)
- B. 2.414 x 10\(^3\)
- C. 2.414 x 10\(^4\)
- D. 2.414 x 10\(^5\)


