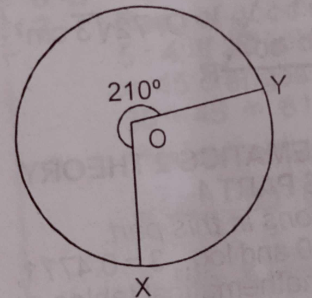
In the diagram above, O is the centre of the circle. Reflex angle XOY = 210º and the length of the minor arc is 5.5m. Find, correct to the nearest metre the length of major arc.
- A. 8m
- B. 9m
- C. 10m
- D. 13m
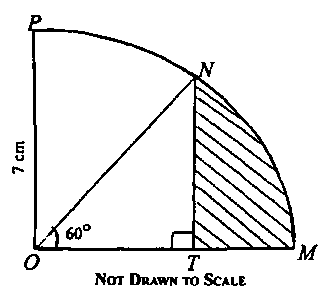
a. In the diagram above, the radius of the sector of circle centre O is 7 cm and ∠MON is 60°. Find, correct to one decimal place, the area of the shaded portion. (take \(\pi = \frac{22}{7})\)
b. The x and y intercepts of a straight line are \(\frac{-3}{4} and \frac{2}{7}\) respectively. Find the equation of the line.

a. In the diagram above P, Q, R, and S are points on the circle with centre O.
QR // OS , ∠QOR = 2m, ∠QPR = n and ∠SOR = 54°. Find the values of m and n.
b. The length of a rectangle is 4 cm more than the width. If the perimeter is 40 cm, find the area.
a. Two regular polygons P and Q are such that the number of sides of P is twice the number of sides of Q. The difference between the exterior angle of P and Q is 45°.find the number of sides of p.
b. The area of a semi-circle is 32π \(cm^2\). Find, in terms of π, the circumference of the semi-circle.
a. In a town, Chief X resides 60 m away on a bearing of 057° from Palace P, while Chief Y resides on a bearing of 150° from the same Palace P. The residence of X and Y are 180 m apart. Illustrate the information in a diagram.
b. Find and correct to three significant figures, the: i. bearing of X from Y; ii. distance between P and Y.
a. The table shows the height of teak trees harvested by a farmer: Find the median height.
| Height(m) | 3 | 4 | 5 | 6 | 7 | 8 |
| number of trees | 4 | 6 | 4 | 5 | 6 | 2 |
b. calculate and correct to one decimal place the: i. mean; ii. standard deviation.
a. Copy and complete the tables of values of y = \(2x^2 – x – 4\) for -3 ≤ x ≤ 3
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 17 | -4 |
b. Using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 2 unit on the y-axis, draw the graph of y = \(2x^2 – x – 4\) for -3 ≤ x ≤ 3.
ci. Use the graph to find: the roots of the equation \(2x^2 – x – 4\)
ii. Use the graph to find the: values of x for which y increases as x increases;
iii. Use the graph to find the: minimum point of y.
a. The sum of three numbers is 81. The second number is twice the first. given that the third number is 6 more than the second, find the numbers.
b. Give me the points P(3, 5) and Q(-5, 7) on the Cartesian plane such that R (x, y) is the midpoint of PQ, find the equation of the line that passes through R and perpendicular to line PQ.
a. M = {n: 2n – 3 ≤ 37} Where n is a counting number. i). write down all the elements in M.
ii. If a number is selected at random from M what is the probability that it is a:
(α) multiple of 3;
(β) factor of 10.
b. A shop owner gave an end-of-year bonus to two of his attendees, Kontor and Gapson in the ratio of their ages. Gapson’s age is one and a half times that of Kontor who is 20 years old. if Kontor received Le 200,000.00, find: i). Find the total amount shared.
ii. Find Gapson’s share.
a. A boy stands at the point M on the same horizontal level as the foot, T of a vertical building. He observes an object on the top, P of the building at an angle of elevation of 66°. He moves directly backward to a new point C and observes the same object at an angle of 53°. if | MT | = 50 m:
Illustrate the information in a diagram;
bi. Calculate and correct to one decimal place: the height of the building;
bii. Calculate and correct to one decimal place: LINE MC.
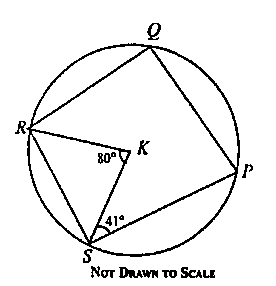
a. In the diagram above, P, Q, R, and S are points on the circle with centre K. KR is a bisector of angle ∠SRQ, ∠KSP = 41°, and ∠SKR = 80°. Find:
∠RQP;
b. Find ∠SPQ
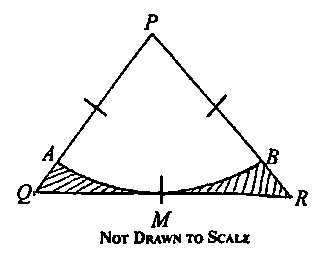
a. In the diagram above, PQR is an equilateral triangle of side 18 cm. M is the midpoint of QR. An arc of a circle with center P touches QR at M and meets PQ at A and PR at B. Calculate, correct to two decimal places, the area of the shaded region. (take \(\pi = \frac{22}{7})\)
a. In a football match, tickets for children and adults were sold at D3.00 and D5.00 respectively. if 400 people attended a football match and D1700.00 was collected in ticket sales. How many tickets were sold to adults?
b. Mr Johnson sold 250 tickets. If 175 of the tickets were for adults, how much sales did he make altogether?
a. A car travels a distance of 112 km at an average speed of 70 km/h. it then travels a further 60 km at an average speed of 50 km/h. Calculate, for the entire journey, the total time taken.
b. if \(\frac{x}{y}\) = 2 and \(\frac{y}{z}\) = 3, find the value of \(\frac{ x + y}{y + z }\)
Find the mean deviation of assets of numbers: 14, 15, 16, 17, 18, and 19.
- A. 2.5
- B. 1.7
- C. 1.5
- D. 3.5
M varies jointly as the square of n and square root of q. If M = 24 when n = 2 and q = 4, find M when n = 5, q = 9.
- A. 288
- B. 400
- C. 300
- D. 225
The diagonals of a rhombus are 16 cm and 12 cm find the length of the side.
- A. 20cm
- B. 8cm
- C. 14cm
- D. 10cm
If 2x – 3y = -11 and 3x + 2y = 3, evaluate \( (y – x)^2\)
- A. 16
- B. 25
- C. 9
- D. 4
A notebook of length 15 cm was measured to be 16.8 cm, calculate, correct to two d.p, the percentage error in the measurement.
- A. 12.00%
- B. 11.71%
- C. 10.71%
- D. 11.21%
Find the gradient of the line passing through the points \((\frac{1}{2}, \frac{- 1}{3}) and ( 3 , \frac{2}{3})\)
- A. \(\frac{2}{5}\)
- B. \(\frac{5}{2}\)
- C. \(\frac{2}{7}\)
- D. \(\frac{7}{2}\)
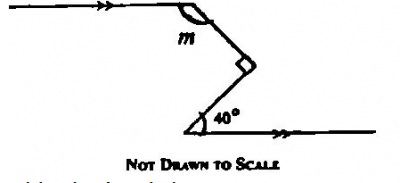
Find the value of m in the diagram above.
- A. \(40^0\)
- B. \(50^0\)
- C. \(130^0\)
- D. \(140^0\)


