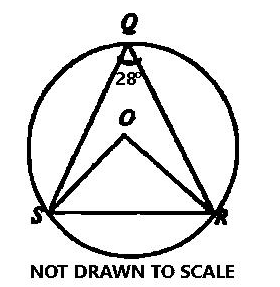
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
- A. \(56^0\)
- B. \(28^0\)
- C. \(76^0\)
- D. \(62^0\)
(a) The diameter of a cylinder closed at both ends is 7cm. If the total surface area is 209cm\(^2\), calculate the height. [Take pi = 22/7].
(b) The points X and Y, 19m apart are on the same side of a tree. The angles of elevation of the top, T, of the tree from X and Y on the horizontal ground with the foot of the tree are 43º and 38° respectively.
(i) Illustrate the information in a diagram. (ii) Find, correct to one decimal place, the height of the tree.
(a) The probability that an athlete will not win any of three races is 1/4.If the athlete runs in all the races, what is the probability that the athlete will win;
(i) only the second race; (ii) all the three races; (ii) only two of the races?
(b) A cone with perpendicular height 24cm has a volume of 1200cm\(^3\). Find the volume of a cone with same base radius and height 84cm. [Take pi = \(\frac{22}{7}\)]

(a) In the diagram, O is the centre of the circle XYZ. angle ZXO=34 ° and angle XOY=146 ° . Find angle OYZ.
(b) The exterior angles of a polygon are 42, 38,57, x, (x+ y)°. (2x- 15)° and (3x -y)º? If x is 7 less than y, find the values of x and y.
| Age | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of children | 2 | 6 | 5 | x | 6 | 9 | 8 | 5 |
The table shows the distribution of ages of a number of children in a school. If the mean of the distribution is 7, find the;
(a) value of x, (b) standard deviation of their ages.
(a) Copy and complete the table of values for y = 3Sinx + 7Cosx for 0°
| xº | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
| y | 7.0 | 4.2 | -0.9 |
(b) Using a scale of 2cm to 20° on the x-axis and 2cm to 2 units on the y-axis, draw the graph of y = 3Sinx + 7Cosx for 0°
(c) Using the graph, find the;
(i) value of y when x= 150°,
(i) range of values of x for which y > 0.
| Item | food & drinks | fuel | rent | building project | education | savings |
| Percentage% | 35 | 7.5 | 1.0 | 15 | 17.5 | x |
The table shows the monthly expenditure (in percentages) of Mr. Okafor’s salary.
(a) Calculate the percentage of Mr. Okafor’s salary that was put into savings.
(b) Illustrate the information on a pie chart.
(c) If Mr. Okafor’s annual gross salary is $28,800.00 and he pays tax of 12%.
Calculate; (i) his monthly tax; (ii) the amount saved each month.
(a) A man purchased 180 copies of a book at N250.00 each. He sold y copies at N300.00 each and the rest at a discount of 5 kobo in the Naira of the cost price.
If he made a profit of N7,125.00, find the value of y.
(b) A trader bought x bags of rice at a cost C = 24x + 103 and sold them at a price, S = \(\frac{x^2}{20} – 33x\).
Find the expression for the profit (i) If 20 bags of rice were sold,
(ii) calculate the percentage profit.
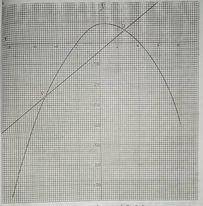
The graph shows the relation of the form y = mx\(^2\) + nx + r, where m, n and r are constants.
Using the graph:
(a) state the scale used on both axes; (b) find the values of m, n and r; (c) find the gradient of the line through P and Q; (d) state the range of values of x for which y > Q.
a) Given that m = tan 30º and n = tan 45º, simplify, without using calculator, \(\frac{ m – n}{mn}\), leaving the answer in the form p + \(\sqrt{q}\)
b) There are 20 women in a bus. 15 of them wear glasses and 10 wear wristwatches. If a woman is chosen at random from the bus, find the probability that she wears both glasses and wristwatches.
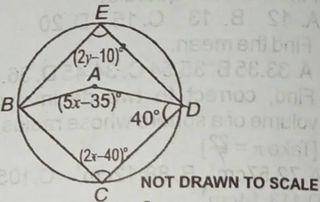
In the diagram, BCDE is a circle with centre
A. ∠BCD = (2x + 40)°, ∠BAD = (5x – 35)º, ∠BED = (2y+ 10)° and ∠ADC=40″. Find:
(a) the values of x and y;
A chord subtends an angle of 72º at the centre of a circle of radius 24.5m. Calculate the perimeter of the minor segment. [Take π = \(\frac{22}{7}\)
Given that y =(\(\frac{pr}{m} – p^2r\))\(^{\frac{-3}{2}}\)
(a) make r the subject;
(b) find the value of r when y = -8, m = 1 and p = 3.
(a) Given that (7 -2x), 9, (5x + 17) are consecutive terms of a Geometric Progression (G. P) with common ratio, r>0, find the values of x.
(b) Two positive numbers are in the ratio 3:4. The sum of thrice the first number and twice the second is 68. Find the smaller number.
Solve 6x\(^2\) = 5x – 1
- A. x = 2,3
- B. x = 0,3
- C. x = \(\frac{1}{2}\), \(\frac{1}{3}\)
- D. x = \(\frac{1}{2}\), \(\frac{-1}{3}\)
Given that log\(_3\) 27 = 2x + 1, find the value of x.
- A. 0
- B. 1
- C. 2
- D. 3
A trader made a loss of 15% when an article was sold. Find the ratio of the selling price : cost price
- A. 3:20
- B. 3:17
- C. 17:20
- D. 20:23
If the equations x\(^2\) – 5x + 6 = 0 and x\(^2\) + px + 6 = 0 have the same roots, find the value of p.
- A. 5
- B. 6
- C. -5
- D. -6
The straight line y = mx – 4 passes through the point(-4,16). Calculate the gradient of the line
- A. -5
- B. -3
- C. 3
- D. 5
The mean of two numbers x and y is 4. Find the mean of four numbers x, 2x, y and 2y
- A. 2
- B. 4
- C. 6
- D. 8
A rectangle with width \(\frac{3}{4}\)cm and area 3 \(\frac{3}{8}\)cm\(^2\). Find the length
- A. 6cm
- B. 4\(\frac{1}{2}\)cm
- C. 2 \(\frac{5}{8}\)cm
- D. 12cm


