(a) Using a suitable diagram, explain how the following can be obtained from a velocity-time graph (i) acceleration; (ii) retardation; (iii) total distance covered.
(b) Show that the displacement of a body moving with uniform acceleration a is given by \(s = ut + \frac{1}{2} at^{2}\) where u is the velocity of the body at time t = 0.
(c) A particle moving in a straight line with uniform deceleration has a velocity of 40ms\(^{-1}\) at a point P, 20ms\(^{-1}\) at a point Q and comes to rest at a point R where QR = 50m. Calculate the: (i) distance PQ; (ii) time taken to cover PQ; (iii) time taken to cover PR.
Explanation
(a) 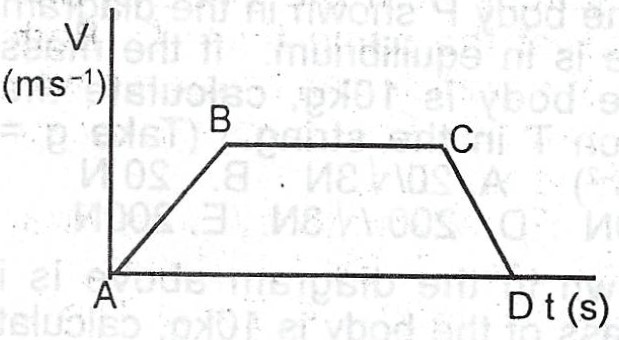
Velocity- time graph:
(i) Acceleration : Gradient of AB in the graph above; (ii) retardation: Gradient of CD in the graph above; (iii) total distance covered is the area under the graph.
(b) S = average velocity x time
\(S = (\frac{u +v}{2}) \times t ... (1)\)
but \(v = u + at ... (2)\), substitute (2) in (1)
\(S = (\frac{u + u + at}{2}) \times t\)
\(S = (\frac{2u + at}{2}) \times t \)
\(S = ut + \frac{1}{2} at^{2}\)
(c) P ----------- Q ----50m------- R
40 ms\(^{-1}\) 20 ms\(^{-1}\)
Since the acceleration is uniform and using equation
\(v^{2} = u^{2} + 2as\) for the motion along QR.
\(0 = 20^{2} - 2a(50)\) (retardation)
\(0 = 400 - 100a \implies 100a = 400\)
\(a = 4 ms^{-2}\) (retardation, hence it is negative)
\(20^{2} = 40^{2} + 2(-4) s\)
\(400 = 1600 - 8s \implies 8s = 1200\)
\(s = 150m\)

