(a) Define the apparent cubic expansivity of a liquid
(b)(i) Describe with the aid of a labelled diagram, an experiment to determine the apparent cubic expansivity of a liquid.
(ii) State two precuations that should be taken to ensure accurate results.
(c) A density glass bottle contains 44.25g of a liquid at 0°C and 42.02g at 50°C. Calculate the real cubic expansivity of the liquid. (Linear expansivity of glass = 1.0 x 10-5K\(^{-1}\))
Explanation
(a) The apparent cubic expansivity of a liquid is defined as the apparent increase in volume per unit volume per unit rise in temperature.
(b)(i)
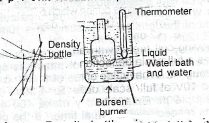
Procedure: Density bottle dried and weighed, M,, fill bottle with liquid, replace the stopper and wipe the bottle dry. Weigh bottle and content M\(_2\), suspend the bottle with content in a water bath. Record the initial temperature of the water in the bath T\(_1\). Then heat water gradually up to boiling point. Notice that some liquid is expelled through the orifice of the stopper and the water in the bath is allowed to continue boiling until no more liquid is expelled through the orifice of the stopper.Record the final temperature T\(_2\) of the water bath. Remove the bottle from the bath, allow it to cool, wipe, dry it and reweigh M\(_3\).
Calculation: Mass of the liquid expelled from the bottle = (M\(_2\) - M\(_3\)) Mass of the liquid left in the bottle = (M\(_3\) - M\(_1\) Temperature change, (T\(_2\) - T\(_1\)) Apparent cubic expansivity
\(\alpha\) a = \(\frac{\text{Mass of the liquid expelled}}{\text{ Mass of remaining liquid \times change in temperature}}\)
\(\alpha\) a = \(\frac{M_2 - M_3}{(M_3 - M_1) - (T_2 - T_1)}\)
(ii) Precautions;
(1) Avoid parallax in reading thermometer
(2) Bottle should not be submerged
(c) Apparent cubic expansivity
\(\alpha\) a = \(\frac{M_2 - M_3}{(M_3 - M_1) - (T_2 - T_1)} = \frac{44.25 - 42.02}{42.02 \times 50}\)
\(\alpha\) a = 1.06 x 10\(^{-3} k^{-1}\)
But real cubic expansivity = \(\alpha\) a =+ \(\alpha\) g
Where \(\alpha\) g is the cubic expansivity of the containing vessel i.e. glass
\(\alpha\) a = 1.09 x 10\(^3 K^{-1}\)

