(a) Explain what is meant by the statement: The capacitance of a parallel-plate capacitor is 2\(\mu\)F
(b) State: (i) three factors on which its capacitance depends
(ii) three uses of capacitors.
(c) Derive a formula for the energy W stored in a charged capacitor of capacitance C carrying a charge Q on either plate.,
(d) Two parallel-plate capacitors of capacitances 2\(\mu\)F and 3\(\mu\)F are connected in parallel and the combination is connected to a 50V d.c. source. Draw the circuit diagram of the arrangement and determine the:
(i) charge on either plate of each capacitor
(ii) potential difference across each capacitor
(iii) energy of the combinad capacitors.
Explanation
3(a) This means that the ratio of the charge on the capacitor to the potential difference between the plates is 4LF.
(b)(i) (1) Area of plates
(2) Dielectric between plates
(3) Distance between plates
(b)(ii) (1) To separate a.c from d.c.
(2) To control current in a.c circuit
(3) To store charges or energy
(c) Workdone, W = QV
Average work done is given by \(\frac{1}{2}\) x QV .........(i)
But V = \(\frac{Q}{V}\) ...............(ii)
Substituting (ii) in (i)
W = \(\frac{1}{2}\) x Q x \(\frac{Q}{C}\)
Energy stored W = \(\frac{1}{2} \times \frac{Q^2}{2} \frac{1}{2} \frac{Q^2}{C}\)
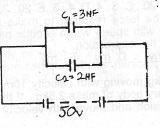
(i) Q\(_2 = C_2V\)
= 100 x 10\(^{-6}\) C = 100\(mu\)C
\(Q_1 = C_1 V\)
= 3 10\(^{-6}\) x 50 = 150\(\mu\)C
(iii) P.d across each capacitor is 50V
(iii) E = \(\frac{1}{2} CV^2\) Since capacitors are in parallel
C = \(\frac{1}{2}\) x 5 \(\mu\)F x 50 x 50
= \(\frac{1}{2}\) x 5 x 10\(^{-6}\) x 50 x 50 = 6.25 x 10\(^{-3}\)J

