Physics JAMB, WAEC, NECO AND NABTEB Official Past Questions

Connect the circuit as shown above. Set the value of R= 30\(\Omega\). Close the key and obtain a balance at point T on the potentiometer wire PQ. Read and record the length TQ = L Evaluate L\(^{-1}\) and R\(^{-1}\), Repeat the experiment for R= 20, 10.5, 3 and 1\(\Omega\) respectively. In each case, determine and record the corresponding values of LL\(^{-1}\) and R\(^{-1}\). Remove the resistance box from the circuit and then determine the length L\(_{o}\) corresponding to R= 0. Tabulate your readings. Plot a graph at R\(_{1}\) on the vertical axis, and L\(^{-1}\) on the horizontal axis, starting both axes from the origin (0,0). Determine the slope, s of the graph and its intercept, I on the vertical axis.
Evaluate: (i) k = 1\(^{-1}\)
                (ii) \(\frac{Lo}{S}\)
State two precautions taken to ensure accurate result

(b)i. Using your graph, determine the value of L for which R =15\(\Omega\).

ii. if the intercept I = 0.5+ y\(^{-1}\), use your graph to determine the value of y.

iii. Explain what is meant by the e.m.f.of a cell.

Trace the outline PQRS of the glass block on a sheet of paper, as shown in the diagram. Remove the block Mark a position 0 very close to P. Draw the normal NOG From point G, measure and mark out Points B\(_{1}\) B\(_{2}\) B\(_{3}\) B\(_{4}\) and B\(_{5}\) along with line GR at distances 1, 2, 3, 4 and 5cm respectively from G. Replace the glass block on the outline PORS Erect a pin at 0 and another at B\(_{1}\). Now fx a pin at T\(_{1}\) such that the pins at T\(_{1}\) and B\(_{1}\) are in line with the pin at O when viewed through the side SR of the glass block. Remove the glass block. Join the line OB\(_{1}\) and B\(_{1}\)T\(_{1}\). Measure and record the angles x and y. Evaluate sin x and y. Repeat the experiment with the pin at B\(_{1}\) fixed at B\(_{2}\), B\(_{3}\), B\(_{4}\) and B\(_{5}\) respectively while the pin at O remains unaltered. In each case, measure and record the values of x, y, sin x, and cos y. Tabulate your readings. Plot a graph of sin x on the vertical axis and cos y on the horizontal.axis, starting both axes from the origin (0,0). Calculate the slope, s of the graph. Evaluate K= \(\frac{1}{s}\). State two precautions taken to ensure accurate results. [Attach your tracings to your answer booklet]

(b)i. State Snell’s law of refraction and explain why reaction Occurs at the boundary between two media.

ii. Differentiate refraction from diffraction.

iii. State two conditions necessary for total internal reflection to occur in a medium.

You are provided with a uniform metre rule, a knife edge and a body m of mass 50g. Suspend the given body m by means of a thread from 1.0cm mark of the metre rule. Balance the loaded metre rule on the knife-edge as shown in the diagram above. Determine and record the value of x when the metre rule is in horizontal equilibrium. Evaluate \(\frac{1}{x}\). Repeat the experiment for values of m = 70, 90, 110, 130 and 150g respectively. In each case, determine and record the corresponding values of x and \(\frac{1}{x}\). Tabulate your readings. Plot a graph of m on the vertical axis and \(\frac{1}{x}\) on the horizontal axis, starting both axes from the origin (0,0). Determine the slope s, of the graph and the value of m for which /\(\frac{1}{x}\) = 0. State two precautions taken to ensure accurate results.

(b)i. Using your graph, determine the value of x for which m = 0.

(ii) State two conditions necessary to maintain the metre rule in the experiment above, in equilibrium.

(iii) Using your graph, determine the value of x for which m = 100g.

(a) Explain the term photoelectric effect.
(b)

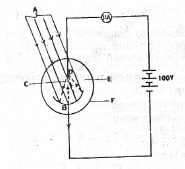
The diagram above represents a photocell with its associated electric circuit. Identify each of the physical quantities
represented by the letters A, B, C, D, E and F

(c) What factor determines the: (i) current produced by the photocell

(ii) maximum kinetic energy of the photoelectrons?

(d) State one similarity and one difference between photoemission and evaporation

(e) Name two methods by which a beam of free electrons may be produced other than photoemission

(f) State two applications of photoelectric effect.

(g) A light wavelength 5.0 x 10\(^{-7}\) m is incident on metal resulting in photoemission of electrons. If the work function of the metal is 3.04 x 10\(^{-19}\)J, calculate the:

(i) frequency of the light

(ii) energy of the incident photon,

(iii) maximum kinetic energy of the photoelectrons (Speed of light = 3.00 x 108ms\(^{-1}\); Planck’s constant = 6.6 x 10\(^{-34}\)Js).

(a)(i) Describe, with the aid of a circuit diagram, an experiment to measure the resistance of a wire given an ammeter of low resistance, a battery, a key, a rheostat, va high-resistance voltmeter and some connecting wires.

(ii) State two precautions necessary to obtain an accurate result.

(b) Using the experimental result and any necessary measurements, explain how the resistivity of the wire may be determined.

(c) Two cells, each of e.m.f. 2V and internal resistance 0.552, are connected in series. They are made to supply current to a combination of three resistors, one of resistance 20 connected in series to a parallel combination of two other resistors each of resistance 3Q. Draw the circuit diagram and calculate the:

(i) current in the circuit

(ii) potential difference across the parallel combination of the resistors

(iii) lost volts of the battery.

(a) Distinguish between heat and temperature.

(b) State two physical properties of substances which may be used to measure temperature.

(c) State two reasons why mercury is preferred to alcohol as a thermometric liquid.

(d)(i) Describe how a mercury-in-glass thermometer is calibrated.

(ii) State two precautions necessary to ensure an accurate result.

(e) Explain how land and sea breezes occur.

(a) Explain the term uniform acceleration

(b)(i) Sketch and describe the velocity-time graph for the motion of a ball from the time it is projected vertically upwards until it returns to the point of projection.

(ii) Neglecting air resistance and using ycur sketch, explain how the acceleration of free fall due to gravity g, and the maximum height attained when the ball is projected vertically upwards can be determined.

(c) A stone is projected vertically upwards with a velocity of 20ms\(^{-1}\). Two seconds later, a second stone is similarly projected with the same velocity. When the two stones meet, the second one is rising at a velocity of 10ms\(^{-1}\). Neglecting air resistance, calculate the:

(i) length of time the second stone is in motion before they meet,

(ii) velocity of the first stone when they meet (Take g as 10ms\(^{-2}\))
 

It is always not possible to determine exactly and simultaneously the position and momentum of a particle. This statement is known as the

Two radioactive elements X and Y have half-lives of 100 and 50 years respectively. Samples of X and Y initially contain equal number of atoms. What is the ratio of the number of the remaining atoms of X to that of Y after 200 years?

The frictional effect between the layers of a moving fluid is called

A radioactive nuclide of proton number X emits a \(\beta\)-particle to form a new nuclide to proton number Y. The correct equation relating X and Y is

The process of increasing the energy of an atom via inelastic collision with an electron is known as

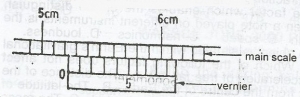
The diagram above represents a section of a pair of vernier calipers. The reading on the instrument is

When light from a source is sent through a gas
I. Certain wavelengths are absorbed.
II. an emission line spectrum results.
III. A dark line is left.
Which of the following is/are correct?

An electron is accelerated from rest through a potential difference of 70kV in a vacuum. Calculate the maximum speed acquired by the electron (electronic charge = -1.6 x 10^-19; mass of an electron = 9.1 x 10^-31kg)

Which of the following explains the concave meniscus of water in a clean glass tube? the

Use the following data to determine the length L of a wire when a fore of 30N is applied, assuming Hooke’s law is obeyed
\(\begin{array}{c|c}\text{Force applied/N} & 0 & 5 & 10 & 30\\ \hline \text{length of wire/mm} & 500.0 & 500.0 & 501.0 & L \end{array}\)

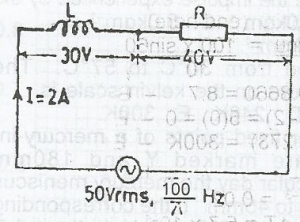
The diagram below illustrates an a.c.source of 50V(r.m.s.), \(\frac{100}{\pi}\)Hz connected in series with an inductor of inductor of inductance L and a resistor of resistance R. The current in the circuit is 2A and the p.d across L and R are 30V and 40V respectively. Calculate the average power dissipated in the circuit

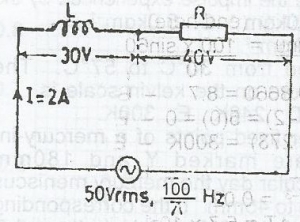
The diagram below illustrates an a.c.source of 50V(r.m.s.), \(\frac{100}{\pi}\)Hz connected in series with an inductor of inductor of inductance L and a resistor of resistance R. The current in the circuit is 2A and the p.d across L and R are 30V and 40V respectively. Calculate the power factor of the circuit

The direction of the magnetic field at a point in the vicinity of a bar magnetic is

A proton of charge 1.6 x 10\(^{19}\)C is projected into a uniform magnetic field of flux density 5.0 x 10\(^5\)T. If the proton moves parallel to the field with a constant speed of 1.6 x 10\(^6\)ms\(^{-1}\), calculate the magnitude of the force exerted on it by the field