(a) State the conditions of equilibrium for a number of coplanar parallel forces.
(b) A metre rule is found to balance horizontally at the 48 cm mark. When a body of mass 60 g is suspended at the 6 cm mark, the balance point is found to be at the 30 cm mark. Calculate the;
(i) mass of the metre rule;
(ii) distance of the balance point from the zero end, if the body were moved to the 13 cm mark.
(c) a man pulls up a box of mass 70 kg using an inclined plane of effective length 5 m unto a platform 2.5 m high at a uniform speed. If the frictional force between the box and the plane is 1000 N;
(i) draw a diagram to illustrate all the forces acting on the box while in motion;
(ii) calculate the I. minimum effort applied in pulling up the box; II. velocity ratio of the plane, if it is inclined at 30° to the horizontal; Ill. force ratio of the plane.
Explanation
(a) The sum of the clockwise moments about a point = the sum of the anticlockwise moments about the same point
(b)(i)
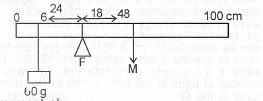
Take a moment about the fulcrum F
60 x 24 = m x 18
m = \(\frac{60 \times 24}{18}\)
= 80g
(ii)
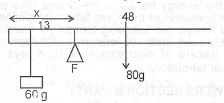
Take a momen about F, 60 x (\(x\) - 13) = 80 x (48 - \(x\))
3(\(x\) - 13) = 4(48 - \(x\))
3\(x\) - 39 = 192 - 4\(x\)
7\(x\) = 231
\(x = \frac{231}{7}\) = 33cm
(c)(i)

(ii)
(i) Minimum effort E = F + mgsin\(\theta\) = 1000 + 700 sin \(\theta\) = 1350N
(ii) V.R = \(\frac{1}{sin \theta} = \frac{1}{sin 30}\) = 2
(ii) M.A = \(\frac{L}{E} = \frac{700}{1350}\) = 0.52

