
You are provided with a uniform meter rule, a knife edge, masses and other necessary apparatus.
- Suspend the metre rule horizontally on the knife edge. Read and record the point of balance G of the métre rule. Keep the knife edge at this point throughout the experiment.
- Using the thread provided, suspend the object labelled W at the 15cm mark of the metre rule.
- Suspend a mass M= 20g on the other side of G. Adjust the position of the mass until the metre rule balances horizontally again.
- Read and record the position Y of the mass M on the metre rule.
- Determine and record the distance L between the mass and G. Also determine and record the distance D between W and G.
- Repeat the procedure for four other values of M = 30, 40, 50 and 60 g. In each casse ensure that W is kept Constant at the 15 cm mark and the knife edge at G.
- Evaluate L\(^{-1}\) in each case. Tabulate your readings.
- Plot a graph of M on the vertical axis against L\(^{-1}\) on the horizontal axis.
- Determine the slope S, of the graph.
- Evaluate \(\frac{4}{D}\)
State two precautions taken to obtain accurate results.
(b)i. State the principle of moments.
ii. Define centre of gravity
Explanation
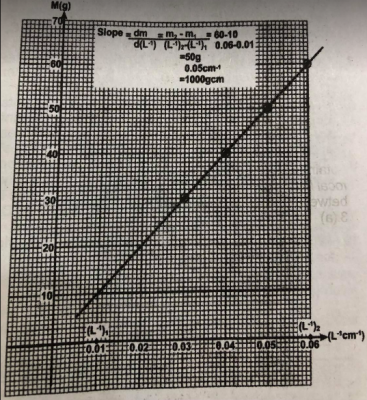
Table of values (observation)
G = 48cm
D = 48 - 15 = 33cm
| S/N | MCg | YCcm | LCcm | DCcm | L\(^{-1}\)Ccm |
| 1 | 20 | - | - | 33.00 | - |
| 2 | 30 | 81.00 | 33.00 | 33.00 | 0.03 |
| 3 | 40 | 72.75 | 24.75 | 33.00 | 0.04 |
| 4 | 50 | 67.80 | 19.80 | 33.00 | 0.05 |
| 5 | 60 | 64.58 | 16.50 | 33.00 | 0.06 |

Slope = dm = m\(_{2}\) - m\(_{1}\) = 60 - 10 = 50g
d(1\(^{-1}\))\(_{2}\) - (1\(^{-1}\))\(_{1}\) = 0.06 - 0.01 = 0.05cm\(^{-1}\)
= 1000gcm
\(\frac{S}{D} = \frac{1000}{33}\) 30.3g
Precautions: i
- Draught was avoided.
- Parallax error on reading metre rule/was avoided.
- Repeated readings (must be shown on table).
- Ensured suspended masses did not touch the table.
(b) The principle of moments states that for a body in equilibrium, the sum of the clockwise moments about a point is equal to the sum of the anticlockwise moments about the same point.
ii. The centre of gravity of a body is the point through which its resultant weight acts.

