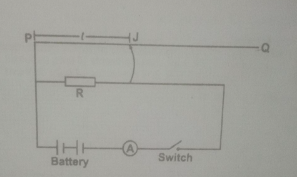
1. Connect the circuit as shown in the diagram above. PQ is a potentiometer wire 100 cm long and R is a standard resistor of 5\(\Omega\).
2. With the jockey J not making contact with PQ, close the switch. Read and record the ammeter reading I. Open the switch.
3. Use the jockey to make contact with PQ at the 20cm mark such that PJ = I = 20 cm. Close the switch, read and record the value I\(_{i}\) of the ammeter. Evaluate I\(^{-1}\).
4. Repeat the procedure for other values of I = 35, 50, 65, and 80 cm. In each case, determine the corresponding values of I\(_{i}\), and I\(^{-1}\). Tabulate your readings.
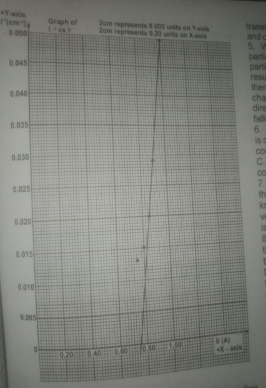
- Plot a graph of I\(^{i}\) on the vertical axis and I\(_{i}\), on the horizontal axis, starting both axes from the origin (0, 0).
- From your graph deduce the value, of I\(_{o}\) of I\(_{i}\), when I\(^{-1}\)= 0.
- Evaluate I\(_{o}\)e
- State two precautions taken to ensure accurate results.
(b)) Define the e. m.f. of a battery
ii. A cell X e.m.f. 1.00 V is balanced by a length of 40.0 cm on a potentiometer wire. Another cell Y is balanced by a length of 60.0 cm on the same wire. Calculate the e.m.f. of Y.
Explanation
| S/N | L(cm) | Ii(A) | L\(^{-1}\)(cm\(^{-1}\)) |
| 1 | 20 | 1.00 | 0.050 |
| 2 | 35 | 0.90 | 0.029 |
| 3 | 50 | 0.85 | 0.020 |
| 4 | 65 | 0.80 | 0.015 |
| 5 | 80 | 0.75 | 0.013 |
When L\(^{-1}\) = 0, Ii = 0.75A
I\(_{o}\) = 75A
\(\frac{I_{o}}{I}= \frac{0.75A}{0.20A}\) = 37.5
SEE THE GRAPH ABOVE...
Precautions: i
- ensured there was no error due to parallax when reading my ammeter.
- ensured that I removed the key after each reading.
(b)i. E.m.f is the total work done in pushing one coulomb of electricity round an external resistor and the internal resistor of the source, or the total energy obtained per coulomb from a cell or battery
ii. \(\frac{Ey}{Ex} = \frac{Iy}{Ix}\)
Iy = 60cm
Ex = 1.00v
Ix = 40.cm
Ey = ?
\(\frac{Ey}{1.00}=\frac{60}{40}\)
Ey = \(\frac{60 \times 1.00}{40}\) = 1.50.v

