(a) Define magnetic line of force.
(b) A wire of length 10 cm carrying a current of 4.0 A is placed between the poles of a powerful electromagnet of magnetic flux density 2.0 T. Calculate the:
(i) force on the wire when it is parallel to the field;
(ii) maximum force on the wire;
(iii) force on the wire when it makes an angle of 60° with the field.
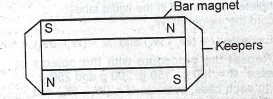
(c) Describe how keepers can be used to preserve the magnetic strength of permanent bar magnets.
(d) A sailor observes that his mariners’ compass reads N 10° W at a place where the angle of declination is N15° W. Calculate the true bearing of the place.
Explanation
(a) Magnetic line of force is defined as an imaginary line in a mangetic field along which a free or isolated north pole would move. OR, it is an imaginary line in a magnetic field such that the targent to it at any point gives the direction of the field at that point.
(b) F = 1BL Sin\(\theta\)
(i) When wire is parallel to the field F = IBL = 4x 2 x 0.1 =0N
(ii) When force is maximum F = IBL Sin90° = 4 x 2 x 0.1 x Sin90°= 0.8N
(iii) When the wire is at 60° to the field
F = IBL Sin\(\theta\) = 4 x 2 x 0.1 x Sin60° = 0.693N
(c) Magnets are stored in pairs with their poles adjacent, placing soft iron pieces called keepers across their ends. The keepers become magnets by induction decreasing the reluctance of the air gap; hence both magnets and keepers form closed loops with no free poles preventing demagnetization
 .
.
(d) True bearing = 15 + 10 = N25°W.

