
Study the diagrams above and use them as guides in carrying out the following instructions.
- Using the spring balance provided, determine the weight of the object of mass M= 50.0g in air. Record this weight as W\(_{1}\).
- Determine the weight of the object when it is completely immersed in water contained in a beaker as shown in the diagram above. Record the weight as W\(_{2}\).
- Determine the weight of the object when it is completely immersed in a liquid labeled L. Record the weight as W\(_{3}\).
- Evaluate U = (W\(_{1}\) – W\(_{2}\)) and V = (W\(_{1}\) -W\(_{3}\)).
- Repeat the procedure with the objects of masses M= 100g, 150g, 200g, and 250g
- In each case, evaluate U = (W\(_{1}\) – W\(_{2}\)) and V = (W\(_{1}\) -W\(_{3}\)).
- Tabulate your readings.
- Plot a graph with V on the vertical axis and U on the horizontal axis.
- Determine the slope, s, of the horizontal graph.
- State two precautions taken to ensure accurate results.
(b)i. State Archimedes’ principle.
ii. A piece of brass of mass 20.0g is hung on a spring balance from a rigid support and completely immersed in kerosene from of density 8.0 x 10\(^{2}\)kgm\(^{-3}\). Determine the readings of the spring balance (g= 10ms\(^{-2}\), density of brass 8.0 x 10\(^{3}\)kgm\(^{-3}\))
Explanation
| M\(_{(g)}\) | W\(_{1}\) | W\(_{2}\) | W\(_{3}\) | U=(W\(_{1}\)-W\(_{2}\)) | V=(W\(_{1}\)-W\(_{3}\)) |
| 50 | 0.50 | 0.43 | 0.45 | 0.07 | 0.05 |
| 100 | 1.00 | 0.90 | 0.88 | 0.10 | 0.17 |
| 150 | 1.50 | 1.30 | 1.33 | 0.20 | 0.17 |
| 200 | 2.00 | 1.73 | 1.75 | 0.27 | 0.25 |
| 250 | 2.50 | 2.15 | 2.20 | 0.35 | 0.30 |
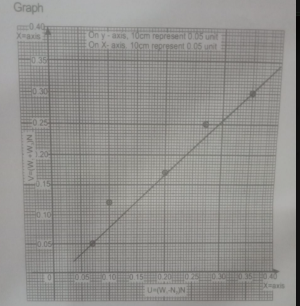
SEE THE GRAPH ABOVE
Slope, s = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{0.275-0.10}{0.32-0.125}\)
s = \(\frac{0.175}{0.195}\) = 0.9
Precautions: i
- ensured that I avoided errors due to parallax while taking the readings on the spring balance.
- made sure the mass is totally immersed in water and liquid
- ensured the retort stand and clamp are well tightened.
(b)i. Archimedes' principle states that when a body is totally immersed in a fluid (liquid or gas), it experiences an upthrust that is equal to the weight of the fluid displaced.
Mass of brass = 20g = 2 x 10\(^{-2}\)kg
Density of kerosine 8.0 x 10\(^{2}\)kgm\(^{-3}\)
g = 10ms\(^{-2}\)kg
Density of brass = 8.0 x 10\(^{3}\)kgm\(^{-3}\)kg
Volume of brass = \(\frac{m}{D} = \frac{2 \times 10}{8 \times 10^{3}}\) = \(\frac{2}{8}\) x 10\(^{-2-3}\)
= 0.25 x 10\(^{-5}\)m\(^{3}\)
Volume of brass = 2.5 x 10\(^{-6}\)m\(^{3}\)
Therefore, the mass of brass in kerosene
m = Density x volume of brass
= 8.0 x 10\(^{2}\) x 2.5 x 10\(^{-6}\)m\(^{3}\)
= 20 x 10\(^{-4}\)
Reading on the spring balance
20 x 10\(^{-4}\) = 20 x 10\(^{-3}\) N

