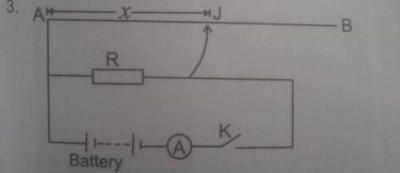
You are provided with a potentiometer AB, a 102\(\Omega\) standard resistor R, a battery of emf 4.5V, a jockey J, and other necessary materials.
- Connect a circuit as shown in the diagram above.
- Close key K. Without J making contact with AB, read and record the ammeter reading I. Open the key.
- Use the jockey to make contact with AB at the 20cm mark such that AJ = x = 20cm. Close the key, read and record the ammeter reading.
- Evaluate x\(^{-1}\).
- Repeat the procedure for values of x= 35cm, 45cm, 60cm, and 80cm respectively.
- Tabulate your readings.
- Plot a graph with x\(^{-1}\) on the vertical axis and l\(_{i}\) on the horizontal axis, starting both axes from the origin (0, 0).
- Determine the slope, s, of the graph.
- From your graph, determine the value l\(_{o}\) of I\(_{1}\) for which x\(^{-1}\)= 0.
- Evaluate \(\frac{I_{o}}{I}\).
- State two precautions taken to obtain accurate results.
(b)i. Define the emf of a battery.
ii. A cell X of emf 1.018V is balanced by a length of 50.0cm on a potentiometer wire. Another cell Y is balanced by a length of 75.0cm on the same wire. Calculate the emf of Y.
Explanation

Electricity
I = 0.36A
| \(\frac{x}{cm}\) | \(\frac{I}{A}\) | \(\frac{X^{-1}}{cm^{-1}}\) |
| 20.0 | 1.14 | 0.050 |
| 35.0 | 0.90 | 0.029 |
| 45.0 | 0.84 | 0.022 |
| 60.0 | 0.78 | 0.017 |
| 80.0 | 0.66 | 0.013 |
Slope (s) = \(\frac{\bigtriangleup {X}^{-1}}{\bigtriangleup {I}}\) = \(\frac{0.08-0.01}{1.68-0.644} = \frac{0.07}{1.036}\)
From the graph,
When X\(^{-1}\) = 0
I\(_{0}\) of I\(_{1}\) = 0.448A
x. Evaluate \(\frac{I_{0}}{I}\)
= \(\frac{0.448}{0.36}\) = 1.244
Precaution;
- The key was opened when readings were not taken.
- I ensured tight connections of the connecting wire
- I avoided parallax errors when reading the potentiometer.
(bi) Define emf of a battery: The e.m.f of a cell is the potential difference across its terminals when it is in an open circuit. i.e. not Supplying current to an external circuit.
ii. A cell x emf is 1.018V.
Length\(_{1}\) on the potentiometer x = 50.0cm
Length\(_{2}\) on the potentiometer, y,= 75.0cm
A cell Y emf is?
Solution
By formula;
\(\frac{E_{1}}{E_{2}}\) = \(\frac{L_{2}}{L_{1}}\)
\(\frac{1.018}{E_{2}} = \frac{75.0}{50.0}\)
75.E\(_{2}\) = 1.018 x 50
E\(_{2}\) = \(\frac{1.018\times 50}{75}\)
E\(_{2}\) = 0.612V.
see graph above

