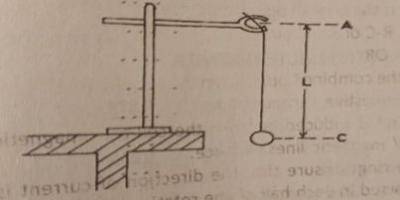
You are provided with a pendulum bob, a metre rule, a stopwatch, a retort stand with clamp, and other necessary apparatus.
i. Suspend the pendulum bob from the clamp as illustrated in the diagram.
ii. Adjust the pendulum such that AC=L= 90 cm
iii. Displace the pendulum bob slightly such that it oscillates in a vertical plane.
iv. Measure and record the time t for 20 complete oscillations.
v. Evaluate T and \(\sqrt L\)
vi.Repeat the procedure for four others values of L= 80 cm,70 cm, 60 cm, and 50cm.
vii. Tabulate your readings
viii. Plot a graph with T on the vertical axis and \(\sqrt L\) on the horizontal axis.
ix. Determine the slope, s, of the graph.
x. Evaluate g= \(\frac{4\pi^{2}}{5^{2}}\)
xi. State two precautions taken to ensure accurate results.
(b) i. Determine from your graph, the period of the pendulum for L= 75 cm.
ii. A simple pendulum bob is set into simple harmonic motion. Sketch a diagram of the setup and indicate on it; the positions of:
(a) maximum velocity.
(b) maximum acceleration of the bob
Explanation
| S/N | L(cm) | t(s) | T = \(\overline{20}\)(S) | \(\sqrt L\) |
| 1 | 90 | 38 | 1.90 | 9.49 |
| 2 | 80 | 36 | 1.80 | 8.94 |
| 3 | 70 | 34 | 1.70 | 8.37 |
| 4 | 60 | 32 | 1.50 | 7.73 |
| 5 | 50 | 30 | 1.50 | 7.07 |
viii. Scale: 2cm rep 0.05 unit on y-axis
2cm rep 1.0 unit on x-axis

ix. Slopes(s) = \(\frac{X_2 - X_1}{Y_2 - Y_1}\)
= (\(\frac{9.9 - 5.7}{2.0 - 1.25}\))
= \(\frac{4.2}{0.75}\)
= 5.6cm
x. Evaluate g = \(\frac{4\pi{^2}}{5^{2}}\)
= \(\frac{4(3.143)^{2}}{(5.6)^{2}}\)
= \(\frac{9.878}{31.36}\)
= 0.315
xi. Precuations:
i. Avoided zero error on stop clock/ metre rule.
ii. Avoided draught.
iii. Avoided conical oscillation
iv. Ensured that support was rigid or firm
v. Ensured bob/pendulum was free from table.
(b)i. \(\sqrt{75cm}\) = 8.66
ii.


