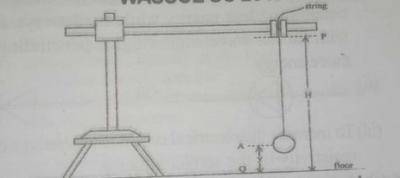
You are provided with a stopwatch, a meter rule, a split cork, retort stand and clamp, a pendulum bob, a piece of thread, and other necessary apparatus.
i. Place the retort stand on a laboratory stool. Clamp the split cork.
ii. Suspend the pendulum bob from the split cork such that the point of support P of the bob is at height H = 100cm above the floor Q. The bob should not touch the floor and H should be kept constant throughout the experiment.
iii. Adjust the length of the thread such that the center A of the bob is at a height y= AQ= 20cm from the floor.
iv. Displace the bob such that it oscillates in a horizontal plane.
v. Take the time t for 20 complete oscillations.
vi. Determine the period T of oscillation and evaluate T
vii. Repeat the procedure for four other values of y = 30cm, 40cm, 50cm, and 60cm. In each case, determine T and T.
viii. Tabulate the results.
ix. Plot a graph of T on the vertical axis and y on the horizontal axis, starting both axes from the origin (0,0).
x. Determine the slope, s, of the graph and the intercept c on the vertical axis.
xi. If in this experiment SR= c, calculate R.
x. State two precautions taken to ensure accurate results.
(b) i. The bob of a simple pendulum is displaced a small distance from the equilibrium position and then released to perform simple harmonic motion Identify where its:
(\(\propto\)) kinetic energy is maximum
(\(\beta\)) acceleration is maximum
ii. An object of weight 120N vibrates with a period of 4.0s when hung from a spring. Calculate the force per unit length of the spring. [g= 10ms\(^{-2}\), \(\pi\)=3.142]
Explanation
H = 100cm
Table of value
| SN | y(cm) | t(sec) | T | T\(^{2}\) |
| 1 2 3 4 5 |
20 30 40 50 60 |
50.50 47.50 43.50 40.00 35.80 |
2.525 2.375 2.175 2.000 1.790 |
6.376 5.641 4.731 4.000 3.204 |
Slope (s) = \(\frac{\bigtriangleup T^{2}}{\bigtriangleup \text{y}}\) = \(\frac{604 - 2.0}{76 - 20}\)
= \(\frac{4.4}{56}\) = 0.079 = 0.08
Intercept on vertical axis = 8
Evaluate R = \(\frac{s}{c}\) = \(\frac{8.00}{0.08}\) = 100

Scale: Let 2cm represent 1 unit on the vertical axis and 1.5cm represent 10 units on the horizontal axis.
Precautions
- Avoided parallax error in reading stopwatch/clock/ meter rule.
- Noted/corrected/avoided zero error on stopwatch/ clock/meter rule.
- Avoided draught/switch off fans.
- Avoided conical oscillation Ensured that support was rigid/firm.
- Ensured bob of the pendulum was free from table/did not touch table
- Repeated reading shown on the table.
- Small angular displacement
(b) (\(\propto\)) The kinetic energy is maximum at the equilibrium position
(\(\beta\)) The acceleration is maximum at the point of maximum displacement.

ii. The period T is given by
T = 2\(\pi\)\(\sqrt\frac{M}{K}\)
T\(^{2}\) = 4\(\pi^2\)\(\frac{M}{K}\)
K = 4\(\pi^2\)\(\frac{M}{T^{2}}\)
= \(\frac{4x(3.14)^2(\frac{120}{10})}{4}^2\)
29.62NM\(^{-1}\)
OR
T = 2\(\pi\)\(\sqrt\frac{e}{g}\)
T\(^{2}\) = 4\(\pi^2\)\(\frac{e}{g}\)
e = \(\frac{T^{2}}g{4\pi^2}\) = 4.05
k = \(\frac{f}{e}\) = \(\frac{120}{4.05}\)
= 29.62NM\(^{-1}\)

