Physics JAMB, WAEC, NECO AND NABTEB Official Past Questions

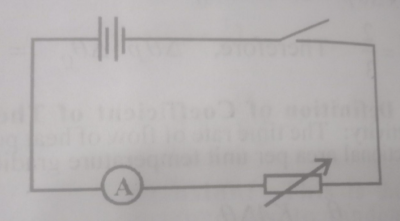
(a) You are provided with a battery, an ammeter, a voltmeter, a resistance box, a key and connection wires.

(i) Set up circuit as shown in the diagram above.

(ii) With the key opened, measure and record the e.m.f. E\(_o\) of the battery

(iii) With the key closed, select the resistance R=1 on the resistance box. Read and record the current, 1Ω.

(iv) Evaluate I\(^{-1}\).

(v) Repeat the procedure for five other values of R=2Ω,3Ω, 4Ω, 5Ω, and 6Ω.

In each case, record I and evaluate I\(^{-1}\) results.

(vii) Plot a graph with R on the vertical axis and I\(^{-1}\) on the horizontal axis.

(Viii) Determine the slope, s, of the graph.

(ix) Determine the intercept C, On the vertical axis.

(x) State two precautions taken to ensure accurate results.

(b)(i) Define potential difference in an electric field.

(ii) A piece of resistance wire of diameter 0.2 mm and length 25 cm has a resistance of 7Ω. Calculate the resistivity of the wire of the battery. [ π = 22\7]

You have been provided with a ray box, a converging lens, a lens holder, a screen, a metre rule, and half- metre rule. Use the diagram above as a guide to perform the experiment.

(i) Determine the approximate focal length f, of the lens by focusing a distant object on the screen.

(ii) Place the ray box and the screen such that the distance between the illuminated cross-Wire and the screen, D= 150 cm.

(iii) Place the lens at a position L where a sharp mage of the cross-Wire Is obtained on the screen Note L.

(iv) Move the lens at a position L, to 0btain another sharp image of the cross-wire on the screen. Note L

(V) Measure the distance, d. between L\(_1\) and L\(_2\).

(Vi) Evaluate D\(^2\): d\(^2\) and D\(^2\) – d\(^2\).

(vii) Repeat the procedure for four other values of D = 130cm, 100 cm, 90 cm and 80 cm. in each case.evaluate D\(^2\); d\(^2\) and D\(^2\) – d\(^2\).

(viii) Tabulate the result

(ix) Plot a graph with D\(^2\) – d\(^2\) on the vertical axis and  D on the horizontal axis.

(x) Determine the r values of D axis and  Determine the slopes, S, of the graph.

(xi) Evaluate k = \(\frac{s}{4}\)

(xii) State two precautions taken to ensure accurate results.

(bi) Distinguish between a virtual image and. plain image?

(ii) With the aid of a ray diagram, explain how a converging lens produces a Virtual image

(a) You are provided with a set of masses, a metre rule, a thread, two retort stands and clamps, a stop watch, a knife edge and split corks.

Carry out the following instructions using the diagram above as a guide.

(i) Determine the centre of gravity, C, of the metre rule using the knife edge.

(ii) Read and record the mass, M, of the metre rule written on the reverse side of it.

(iii) Suspend the metre rule by means of two parallel threads of equal length, h= 70 cm with one at the 10 cm mark and the other at 90 cm mark of the metre rule.

(iv) Attach a mass m = 30g firmly to the metre rule at C. Ensure that the graduated face of the metre rule is facing upwards and that d= 80 cm throughout the experiment. (v) Set the metre rule into small angular oscillations about the vertical axis through its centre of gravity by displacing its ends in opposite directions.

(VI) Determine the time,i, for 20 oscillations and evaluate the period T, T\(^2\) and T\(^{-2}\).

(vii) Repeat the procedure for four other values of m =40 g, 50 g, 60 g and 70 g n each case, determine I and evaluate T\(^2\) and T\(^{-2}\).

(viii) Plot a graph of T on the vertical axis and m on the horizontal axis.

(ix) Determine the slope, s, of the graph.

(x) Evaluate Q= 0.68 / s.

(xi) State two precautions taken to ensure accurate results.

(b) (i) Give two examples of simple harmonic motion other than the motion of a simple pendulum.

(ii) Explain the term centre of gravity of a body.

(a)(i) State the principal factor that determines the relative stability of a radioactive nucleus.

(ii) Arrange the following radioactive nucleus in decreasing order of stability. Justify your answer: X,W and Y: 

\(^40{X}_20\)   \(^920{Y}_36\) and \(^95{Z}_42\)

(b)(i) Explain the term ionization potential.
(ii)

The diagram above illustrates energy levels  in the hydrogen atom. E, is the energy of the E\(_0\) ground state.

(i) When an electron makes a transition from level n = 3 to level n = 1, it emits a photon of wavelength 1.02x 10\(^{-7}\)m. Calculate E\(_0\).

(ii) Calculate the ionization potential of the hydrogen atom.

(c)(i) Explain the statement, the work function of sodium is 2.0 eV. (ii) Light of wavelength 160 mm is shone on the surface of a sodium metal of work function 2.0 eV. Determine whether photoelectrons will be emitted. [h = 6.6 x 10\(^{-34}\) Js, e = 3.0 x 10\(^{8}\)m/s, I eV = 1.6 x 10\(^{-19}\) J]

(a)(i) What is meant by the root-mean-square value of an alternating current? (ii) Define impedance of an alternating current circuit.

(b) An electrical device rated 120 V, 60 W is opened on a 240 V, 50Hz mains supply. The circuit has a capacitor connected in series with ihe electrical device and the supply. Calculate the capacitance of the capacitor. [π=3.142].

(c)(i) Define the capacitance of a capacitor.

(ii)

The circuit diagram above illustrates two capacitors of capacitance C\(_1\) and C\(_2\) connected in series across a 2V source.

(i)Obtain an expression for the total capacitance in terms of C\(_2\). 2 mm 5 n (ii) Calculate the potential difference across each capacitor.

(a)(i) Define each of the following terms as it relates to converging lenses (i) focal length; (ii) optical Centre.

(iii) Draw a ray diagram to illustrate how a converging lens is used to produce a virtual image of an object.

(b)(i) Name the primary colors of light. (ii) Match each primary color to its corresponding complementary color.

(c) A ray passes symmetrically through a glass prism of angle 60° and refractive index of 1.5. Calculate the angle of: (i) incidence; (ii) minimum deviation.

c(ii)
(a)(i) Define dew point. (ii) Explain why dew forms more quickly on the metal parts than on the rubber parts of a bicycle placed in the open overnight.

(b)(i) Explain the statement. the specific heat capacity of copper is 400 J/kg/K. (ii) Two metals, P and Q are supplied with the same quantity of heat.

If the ratio of the specific heat capacity of P to Q is 3: 1 and their masses are in the ratio I:2 respectively.

calculate the ratio of the temperature rise of P to Q.

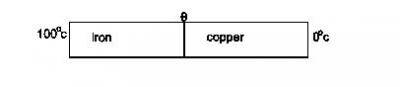
(c)(i) Define coefficient of thermal conductivity of a material.

The diagram above c(ii) illustrates a composite bar of iron and copper. The bar is insulated along its sides and it has a diameter of 10 mm. The length and thermal conductivity of the iron are 0.15 m and 40 W/m/K, respectively and those of copper are 0.05 m and 360 W/m/K, respectively. If the free ends of the iron and copper are kept at 100°C and 0°C respectively. calculate the (i) temperature at the interface between the bars; (ii) rate of heat flow along the bar.

(a)(i) State Hooke’s law. (ii) A spring has a length of 0.20 m when a mass of 0.30 kg hangs on it, and a length of 0.75 nm when a mass of 1.95 kg hangs on it. Calculate the: (i) force constant of the spring; (ii) length of the spring when it is unloaded. [g = 10m/s\(^2\)]

(b)(i) What is diffusion? (ii) State two factors that affect the rate of diffusion of a substance. (iii) State the exact relationship between the rate of diffusion of a gas and its density.
(c) A satellite of mass, m orbits the earth of mass. M with a velocity, v at a distance R from the centre of the earth. Derive the relationship between the period T, of orbit and R.

State three observable phenomena where a particle behaves like waves. State the scientific principle underlying the operation of fibre optics.

(b) Explain each of the following terms as used in fibre optics: (i) core; (ii) cladding

Explain the wave-particle duality of light. (b) A particle of wavelength 4.2x 10\(^{-11}\)m travels (a) With a momentum of 1.6 x 10\(^{-23}\) kg m/s,

Determine the value of the Planck’s constant, h.

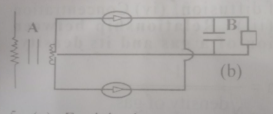
The circuit diagram above is a simple current rectifier circuit. Use it to answer the questions that follow

(a) State the function of each of the parts labeled A and B. Sketch the output signal produces.

A projectile is fired at an angle of 30° to the horizontal with a velocity of 40 m/s Calculate the velocity attained after 1 s. [g = 10 m/s\(^2\)]

(a) Name two artificial satellites.

(b) A geostationary satellite moves in an orbit of radius 6300 km. Calculate the speed with which it moves in the orbit. π = \(\frac{22}{7}\)

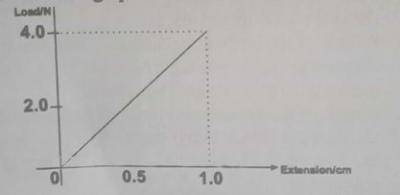
The load-extension graph of an elastic material is illustrated above. Use the graph to determine the work done in stretching the material

Which of the following scientist suggested that moving particles exhibit wave properties?

Which of the following factors is not among that determines the resistance of a wire?

If the relative humidity of the atmosphere increases, the rate of evaporation of sweat from the human body?

Which of the following set of quantities have members which are all vectors?

According to Pascal’s principle, the pressure in a fluid is always?     

A note produced by an instrument is distinguished from a similar note produced by another instrument by the?     

Which of the following statements about distance and displacement is not correct?