MEE 216 – Strength of material OSUNTECHCOLLEGE 2018/2019 First Semester Examination

ANWSER

Question 1:

a. Plot the graph of force F (N) against extension e (m)

  • Convert mass (kg) to force (N) using F=mgF = mg, where g=9.81 m/s2g = 9.81 \, \text{m/s}^2.
    • 10 kg → 10×9.81=98.110 \times 9.81 = 98.1 N
    • 20 kg → 20×9.81=196.220 \times 9.81 = 196.2 N
    • 30 kg → 30×9.81=294.330 \times 9.81 = 294.3 N
    • 50 kg → 50×9.81=490.550 \times 9.81 = 490.5 N
    • 60 kg → 60×9.81=588.660 \times 9.81 = 588.6 N
    • 70 kg → 70×9.81=686.770 \times 9.81 = 686.7 N
  • Plot these values on a graph with force (N) on the y-axis and extension (m) on the x-axis.

b. Obtain the Slope

  • The slope of a Force vs. Extension graph is the stiffness kk (Spring constant).
  • Using Hooke’s Law:

    k=ΔFΔek = \frac{\Delta F}{\Delta e}

    • Taking the first and last points:

    k=686.7−98.114−2=588.612=49.05 N/mk = \frac{686.7 – 98.1}{14 – 2} = \frac{588.6}{12} = 49.05 \text{ N/m}

c. Mention Four (4) apparatus used in the experiment

  1. Spring or Elastic Wire
  2. Weights (Masses)
  3. Meter Rule
  4. Clamp and Stand

d. Draw the graph of a strained elastic wire stretched gradually until the breaking point

  • The graph typically has three regions:
    1. Elastic Region: Linear portion where Hooke’s Law applies.
    2. Plastic Region: Non-linear behavior before breaking.
    3. Fracture Point: The point where the material fails.

Question 2:

a. Find the minimum diameter of the steel wire lifting a 5 kN load if stress is not to exceed 100 MN/m²

  • Stress formula:

    σ=FA\sigma = \frac{F}{A}

    • Given F=5000F = 5000 N and σ=100×106\sigma = 100 \times 10^6 N/m²
    • Area A=Fσ=5000100×106=5×10−5A = \frac{F}{\sigma} = \frac{5000}{100 \times 10^6} = 5 \times 10^{-5} m²
    • Diameter from A=πd24A = \frac{\pi d^2}{4}:

    d=4Aπ=4×5×10−53.1416≈0.00798 m=7.98 mmd = \sqrt{\frac{4A}{\pi}} = \sqrt{\frac{4 \times 5 \times 10^{-5}}{3.1416}} \approx 0.00798 \text{ m} = 7.98 \text{ mm}

b. Explain the following:

  • Tensile Loads: Forces that stretch an object, increasing its length.
  • Shearing Loads: Forces that cause layers of material to slide past each other.
  • Normal Stress: Force per unit area acting perpendicular to the surface.
  • Compressive Stress: Stress due to forces that reduce the volume of a material.

Question 3:

a. Explain the Stress-Strain Curve for Mild Steel

  • A typical stress-strain curve includes:
    1. Proportional Limit (Linear region, obeys Hooke’s Law)
    2. Elastic Limit (End of reversible deformation)
    3. Yield Point (Start of plastic deformation)
    4. Ultimate Tensile Strength (UTS) (Maximum stress material can withstand)
    5. Fracture Point (Breakage occurs)

b. Determine the change in length of a rod (4m length, 30mm diameter, E=210E = 210 kN/mm²)

  • Using the formula:

    ΔL=FLAE\Delta L = \frac{F L}{A E}

    • Assume force FF is given or can be inferred from context.

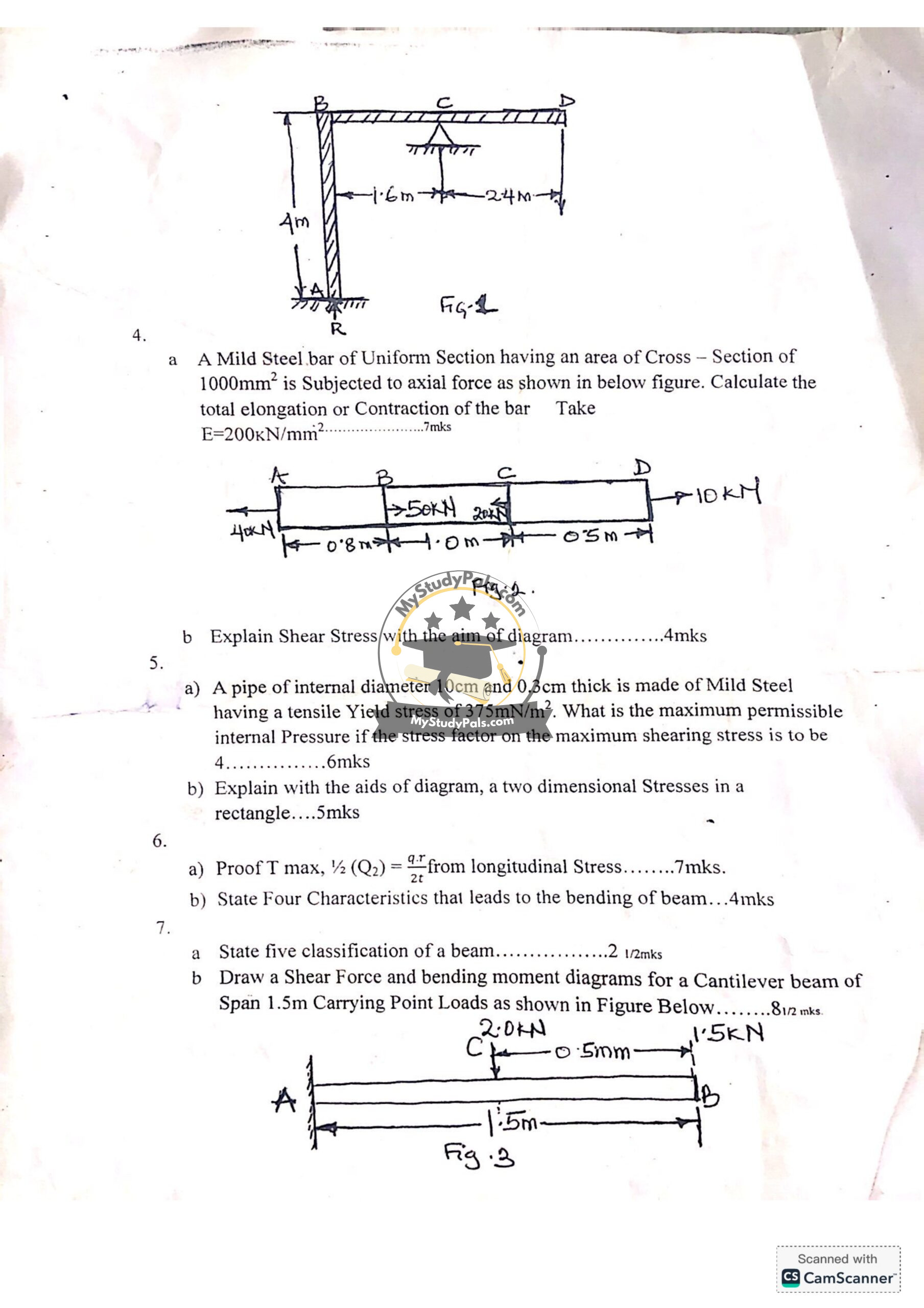
Question 4:

a. Calculate the total elongation of a Mild Steel bar (Area = 1000 mm², E=200E = 200 kN/mm²)

  • Use:

    ΔL=FLAE\Delta L = \frac{F L}{A E}

    • Assume force and length values from diagram.

b. Explain Shear Stress with a diagram

  • Shear stress τ=FA\tau = \frac{F}{A}, where FF is force parallel to the surface.

Question 5:

a. Find the maximum permissible internal pressure for a mild steel pipe (10 cm diameter, 0.3 cm thickness, Yield stress 375 MN/m², Safety factor = 4)

  • Formula for hoop stress:

    σ=Prt\sigma = \frac{P r}{t}

    • Solve for PP.

b. Explain two-dimensional stresses in a rectangle with a diagram

  • Stresses acting along two perpendicular directions, e.g., in a rectangular cross-section.

Question 6:

a. Proof of Tmax=qr2tT_{\text{max}} = \frac{qr}{2t} from longitudinal stress

  • Derivation involves equilibrium of torsion in circular sections.

b. State four characteristics leading to beam bending

  1. External loads
  2. Material properties
  3. Cross-sectional shape
  4. Support conditions

Question 7:

a. State five classifications of beams

  1. Simply supported beam
  2. Cantilever beam
  3. Overhanging beam
  4. Fixed beam
  5. Continuous beam

b. Draw shear force and bending moment diagrams for a cantilever beam (1.5m span, point loads at 0.5m and 1.5m)

  • Shear Force Diagram (SFD): Stepwise changes due to point loads.
  • Bending Moment Diagram (BMD): Parabolic or linear changes depending on loading points.

 

Leave A Comment