ANSWER
Question 1:
a) Differences between one-way ANOVA and one-sample t-test
- One-way ANOVA compares the means of more than two groups to determine if there is a statistically significant difference among them.
- One-sample t-test compares the mean of a single group to a known population mean to determine if there is a significant difference.
b) Definitions of Biometrics Terms
- LD₅₀ (Lethal Dose 50): The dose of a substance that is lethal to 50% of a test population.
- ED₅₀ (Effective Dose 50): The dose at which 50% of a population exhibits the desired therapeutic effect.
- Bioassay: A method of determining the concentration or potency of a substance by its effect on living cells or tissues.
- Clinical Trials: Research studies that test how well new medical approaches work in humans.
c) Assumptions of Hardy-Weinberg Principle
- Large population size
- Random mating
- No mutation
- No migration (gene flow)
- No natural selection
Question 2:
a) Estimate a dose-response curve using transformation X = log₁₀ z
- Convert each dose value (z) into log₁₀(z).
- Plot the transformed values against the responses.
- Fit a regression line to estimate the dose-response curve.
b) Difference between Direct and Indirect Bioassay
- Direct Bioassay: Measures the direct response of an organism to a substance (e.g., drug effects on bacteria).
- Indirect Bioassay: Involves an intermediary factor to measure response, such as measuring enzyme levels instead of direct cell effects.
Question 3:
a) Calculations Based on Hardy-Weinberg Equilibrium
- Phenotypic frequency:
- Total population = 800 + 340 = 1140
- Frequency of tasters = 800 / 1140
- Frequency of non-tasters = 340 / 1140
- Allelic frequency (p and q calculation):
- Assume p = dominant allele frequency, q = recessive allele frequency.
- q² = non-tasters / total population = 340 / 1140
- q = √(340 / 1140)
- p = 1 – q
- Genotypic frequency:
- TT = p²
- Tt = 2pq
- tt = q²
b) Differences Between Event, Trial, and Experiment
- Event: A specific outcome or occurrence.
- Trial: A single instance of an experiment or test.
- Experiment: A series of trials conducted under controlled conditions to test hypotheses.
Question 4:
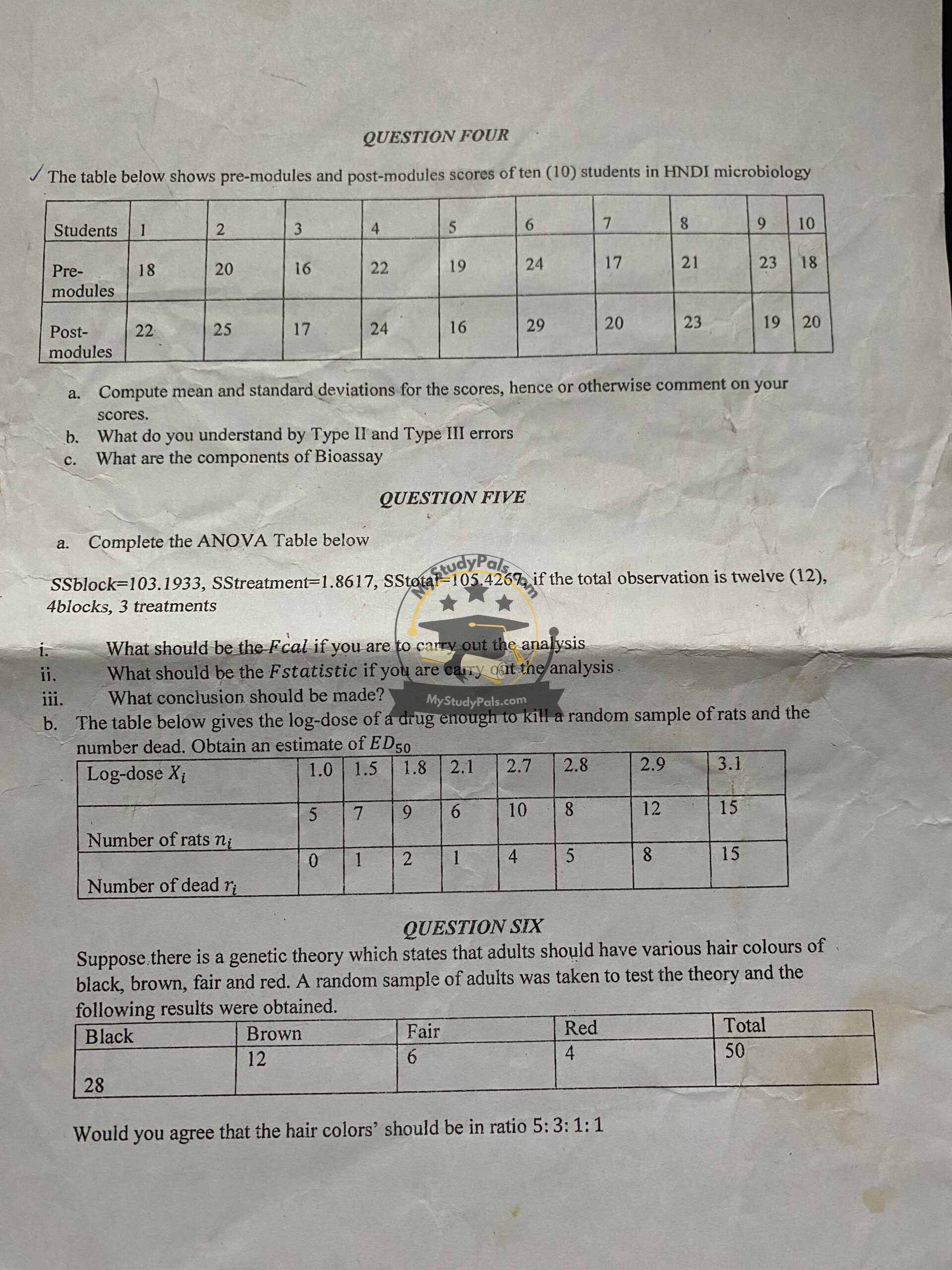
a) Mean and Standard Deviations for Pre-modules and Post-modules Scores
- Compute the mean and standard deviation for both sets of scores using statistical formulas:
- Mean = (Sum of values) / (Number of values)
- Standard deviation formula:
SD=∑(x−xˉ)2NSD = \sqrt{\frac{\sum (x – \bar{x})^2}{N}}
- Compare both values and comment on performance improvements.
b) Type II and Type III Errors
- Type II Error: Failing to reject a false null hypothesis (false negative).
- Type III Error: Correctly rejecting the null hypothesis but answering the wrong question or using the wrong model.
c) Components of Bioassay
- Test organism
- Standard preparation
- Test preparation
- Response measurement
- Statistical analysis
Question 5:
a) ANOVA Table Completion
- Calculate degrees of freedom (df), mean squares (MS), and F-statistic:
- DF for Blocks = number of blocks – 1
- DF for Treatment = number of treatments – 1
- DF for Error = total observations – (blocks + treatments)
- MS = SS / DF
- F-statistic = MS_treatment / MS_error
b) ED₅₀ Calculation
- Use the log-dose and number of dead rats to estimate ED₅₀ using statistical methods such as probit analysis.
Question 6:
- Expected ratios = 5:3:1:1
- Compute expected values for 50 individuals using proportion calculations:
- Black = 510×50\frac{5}{10} \times 50
- Brown = 310×50\frac{3}{10} \times 50
- Fair = 110×50\frac{1}{10} \times 50
- Red = 110×50\frac{1}{10} \times 50
- Compare observed vs. expected values using Chi-square test:
χ2=∑(O−E)2E\chi^2 = \sum \frac{(O – E)^2}{E}
- If Chi-square is below the critical value, the ratio is valid; otherwise, it is not.