(a) Solve the inequality \(\frac{1}{3}x – \frac{1}{4} (x + 2) \geq 3x – 1\frac{1}{3}\)
(b)

In the diagram, ABC is right-angled triangle on a horizontal ground. |AD| is a vertical tower. < BAC = 90\(^o\), < ACB = 35\(^o\), < ABD = 52\(^o\) and |BC| = 66cm.
Find, correct to two decimal places:
(I) the height of the tower
(ii) the angle of elevation of the top of the tower from C
The data shows the marks obtained by students in a biology test
| 52 | 56 | 25 | 56 | 68 | 73 | 66 | 64 | 56 | 48 |
| 20 | 39 | 9 | 50 | 46 | 54 | 54 | 40 | 50 | 96 |
| 36 | 44 | 18 | 97 | 65 | 21 | 60 | 44 | 54 | 32 |
| 92 | 49 | 37 | 94 | 72 | 88 | 89 | 35 | 59 | 34 |
| 15 | 88 | 53 | 16 | 84 | 52 | 72 | 46 | 60 | 42 |
(a) Construct a frequency distribution table using the class interval 0 – 9, 10 – 19, 19, 20, 29…
(b) Draw a cumulative frequency curve for the distribution
(c) Use the graph to estimate the;
(i) median
(ii) Percentage of students who scored at least 66 marks, correct to the nearest whole number.
The force of attraction F, between two bodies, varies directly as the product of their masses, \(m_1\) and m\(_2\) and inversely as the square of the distance, d, between them. Given that F = 20N, when m\(_1\) = 25kg, m\(_2\) = 10kg and d = 5m, find:
(I) an expression for F in terms of m\(_1\), m\(_2\) and d;
(ii) the distance, d for F = 30N, m\(_1\) = 7.5kg and m\(_2\) = 4kg
(b) Find the value of x in the diagram

Three red balls, five green balls, and a number of blue balls are put together in a sack. One ball is picked at random from the sack. If the probability of picking a red ball is \(\frac{1}{6}\) find;
(a) The number of blue balls in the sack
(b) the probability of picking a green ball
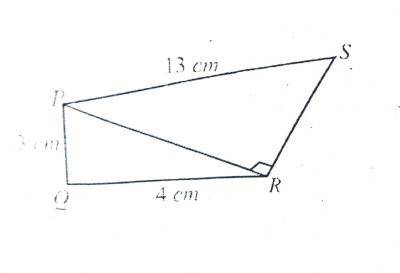
In the diagram, PQRS is a quadrilateral, < PQR = < PRS = 90\(^o\), |PQ| =3cm, |QR| = 4cm and |PS| = 13 cm. Find the area of the quadrilateral.
(a) Ali and Yusif shared N420.000.00 in the ratio 3.,; 5 : 8 respectively. Find the sum of Ali and Yusuf’s shares
(b) Solve: 2(\(\frac{1}{8}\))\(^x\) = 32\(^{x – 1}\).
(a) Find the equation of the line which passes through the points A(-2, 7) and B(2, -3)
(b) Given that \(\frac{5b – a}{8b + 3a} = \frac{1}{5}\) = find, correct to two decimal places, the value \(\frac{a}{b}\)
Evaluate: \(\frac{0.42 \div 2.5}{0.5 \times 2.95}\), leaving the answer in the standard form.
- A. 1.639 x 10\(^2\)
- B. 1.639 x 10\(^1\)
- C. 1.639 x 10\(^{-1}\)
- D. 1.639 x 10\(^{-2}\)
8, 18, 10,14, 18, 11, 13, 14, 13, 17, 15, 8, 16, and 13
The following are scores obtained by some students in a test. How many students scored above the mean score?
- A. 10
- B. 9
- C. 8
- D. 7
The following are scores obtained by some students in a test. Find the median score
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
- A. 14.5
- B. 14.0
- C. 13.5
- D. 13.0
The following are scores obtained by some students in a test, Find the mode of the distribution
| 8 | 18 | 10 | 14 | 18 | 11 | 13 |
| 14 | 13 | 17 | 15 | 8 | 16 | 13 |
- A. 18
- B. 14
- C. 13
- D. 8
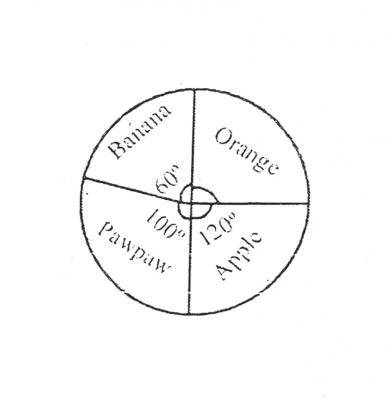
The pie chart represents fruits on display in a grocery shop. If there are 60 oranges on display, how many apples are there?
- A. 90
- B. 80
- C. 70
- D. 40
A box contains 5 red, 6 green and 7 yellow pencils of the same size. What is the probability of picking a green pencil at random?
- A. \(\frac{1}{6}\)
- B. \(\frac{1}{4}\)
- C. \(\frac{1}{3}\)
- D. \(\frac{1}{2}\)
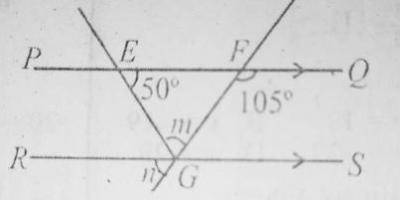
In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of n
- A. 40\(^o\)
- B. 55\(^o\)
- C. 75\(^o\)
- D. 130\(^o\)
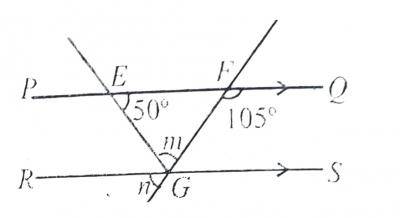
In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of m.
- A. 130\(^o\)
- B. 105\(^o\)
- C. 75\(^o\)
- D. 55\(^o\)
The fourth term of an Arithmetic Progression (A.P) is 37 and the first term is -20. Find the common difference.
- A. 3
- B. 57
- C. 19
- D. 17
Calculate the variance of 2, 4, 7, 8 and 9
- A. 7.2
- B. 6.8
- C. 3.5
- D. 2.6
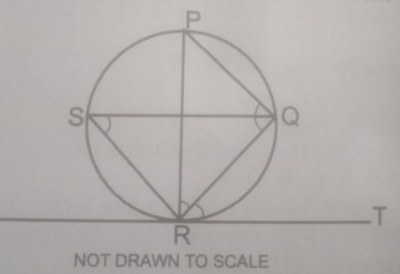
In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Calculate the value of x.
- A. 70\(^o\)
- B. 58\(^o\)
- C. 55\(^o\)
- D. 48\(^o\)
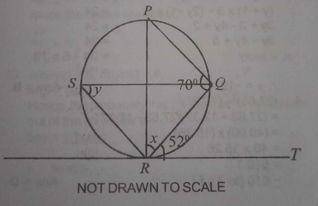
In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Find the value of y.
- A. 70\(^o\)
- B. 60\(^o\)
- C. 52\(^o\)
- D. 18\(^o\)
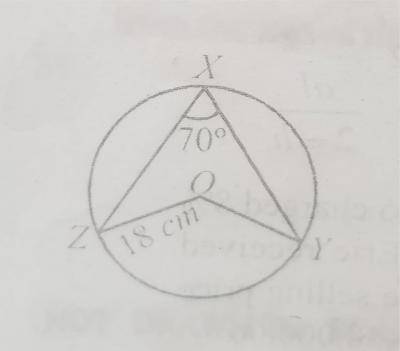
In the diagram, O is the centre of the circle of radius 18cm. If < zxy = 70\(^o\), calculate the length of arc ZY. [Take \(\pi = \frac{22}{7}\)]
- A. 11cm
- B. 22 cm
- C. 44 cm
- D. 80 cm
From the top of a vertical cliff 20m high, a boat at sea can be sighted 75m away and on the same horizontal position as the cliff. Calculate, correct to the nearest degree, the angle of depression of the boat from the top of the cliff.
- A. 56\(^o\)
- B. 75\(^o\)
- C. 16\(^o\)
- D. 15\(^o\)


