If log\(_a\)(y + 2) = 1 + log\(_a\) x, find x in terms of y.
2. The table shows the distribution of timber production in five communities in a certain year
|
Community |
Timber Production (tonnes) |
|
Bibiani Amenfi Oda Wiawso Sankore |
600 900 1800 1500 2400 |
1. Draw a pie chart to represent the information.
2. What percentage of timber produced that year was from Amenfi?
3. If a tonne of timber is sold at $560.00, how much more revenue would Oda community receive than Bibiani?
a) Copy and complete the following table of values for y = 2 cos x – sin x ,\(0^o \leq x \leq 300^o\)
\[\begin{array}{c|c} x & 0^o & 30^o & 60^o & 90^o & 120^o & 150^o & 180^o & 210^o & 240^o & 270^o& 300^o \\ \hline Y & 2.00 & & 0.13 & & -1.87 & & -2.00 & & -0.13 & & \end{array}\]
(b) Using scales of 2 cm to 30\(^o\) on the x-axis and 2cm to 1 unit on the y-axis, draw the graph of y = 2 cos x – sin x for \(0^o \leq x \leq 300^o\)
(c) Use the graph to find the value(s) of x for which:
(i) 2 cos x – sin x = 1;
(ii) tan x = 2.
1. A donkey is tied with a rope to a post which is 15 m from a fence. If the length of the rope between the donkey and the post is 17m, calculate the length of the fence within the reach of the donkey.
2. The base of a right pyramid with vertex, V, is a square, PQRS, of side 15 cm. If the slant height is 32 cm long:
3. represent the information in a diagram;
4. calculate its:
5. height, correct to one decimal place;
6. volume, correct to the nearest \(cm^3\)
(a) Using ruler a pair of compasses only, construct:
(i) a trapezium PQRS such that |PQ| = 6.8 cm, < PQR = 120\(^o\), QR||PS, |PS| =10.6 cm, and IPRI = 93 cm;
(ii) locus \(l_1\) of points equidistant from P and R;
(iii) locus \(l_2\) of points equidistant from Q and R
(b) Measure: (i) |QR|;
ii. < PSR
ii. < PSR
iii. |QY|, where Y is the point of intersection h and h.
A shop had two reduction sales during which prices of all items were reduced by 40% in the first sales and 30% in the second.
- If a shirt was sold at GH₵35.00 during the second reduction sales, find the price before the first sale.
- If the price of an article before the first reduction was GH₵180.00, find the total:
- reduction in the price due to the two sales;
- percentage reduction in the price of the article.
(a) If tan x = \(\frac{5}{12}\), \(0^o\). < x < 90°, evaluate, without using Mathematical tables or calculator, \(\frac{sin x}{(sin x)^2 + cosx}\)
(b) The diagram shows a rectangular lawn measuring 14m by 11m. A path of uniform width \(x\)m surrounds it. If the total area of the path is 186 m\(^2\), how wide is the path?
The table shows the distribution of sources obtained when a fair diwe was rolled 50 times.
| Score | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 2 | 5 | 13 | 11 | 9 | 10 |
1. Draw a bar chart for the distribution
2. Calculate the mean score of the distribution
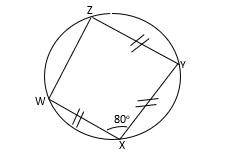
(a) The diagram, = IWYI = IXZI and < WXY = 80\(^o\). What is the size of < XWZ?
(b) A man was charged 2 kobo per month for every N1.00 he borrowed from a bank. At what rate per annum was the interest charged?
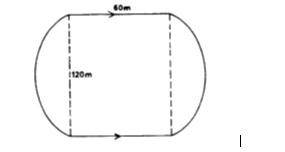
The diagram shows an athletics track with two parallel sides and two semi-circular ends Each of the parallel sides is 60 metres, long and the diameter of each semi-circular end is 120 metres long.
(a) Calculate the distance covered by an athlete who runs round the tack the two times. [Take \(\pi\) = \(\frac{22}{7}\)]
(b) If the athlete spends 200 seconds for the race, calculate the speed in km/h.
Musa is three years older than Manya. Seven years ago, Musa was twice as old as Manya. (1) How old are they now? (2) When will the sum of them be 45?
(a) Evaluate without using calculator, (\(\frac{1}{4} \times 9\frac{1}{7} + \frac{2}{5} (\frac{2}{2} + \frac{3}{4})) \div (\frac{2}{5} – \frac{1}{4})\)
(b) A hunter walked 250 m from point P to Q on a bearing 042\(^o\). Calculate, correct to the nearest meter the vertical distance he has moved.
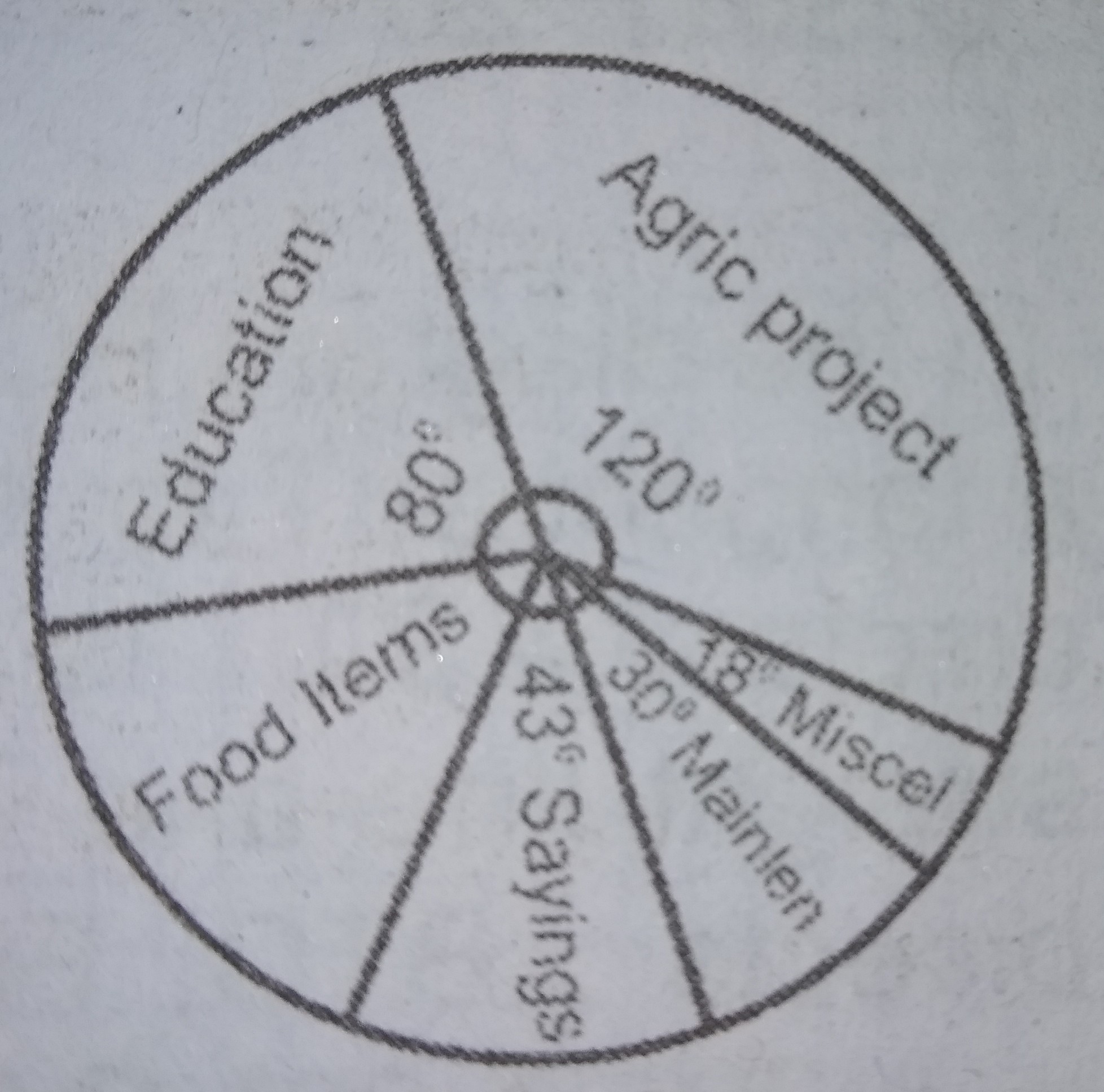
The annual salary of Mr. Johnson Mohammed for 1989 was N12,000.00. He spent this on agriculture projects, education of his children, food items, saving , maintenance and miscellaneous items as shown in the pie chart
How much did he spend on food items?
- A. N9,700.00
- B. N6,700.00
- C. N2,000.00
- D. N4,000.00
- E. N2,300.00
Evaluate \(\frac{2\sin 30 + 5\tan 60}{\sin 60}\), leaving your answer in surd form.
- A. \(\frac{2\sqrt{3}}{3} + 10\)
- B. \(\frac{3\sqrt{2} - 1}{5}\)
- C. \(\frac{3\sqrt{2} + 1}{5}\)
- D. \(\frac{2\sqrt{3}}{3} - 10\)
If \(\sin x = \frac{4}{5}\), find \(\frac{1 + \cot^2 x}{\csc^2 x – 1}\).
- A. \(\frac{13}{2}\)
- B. \(\frac{25}{9}\)
- C. \(\frac{3}{13}\)
- D. \(\frac{4}{11}\)
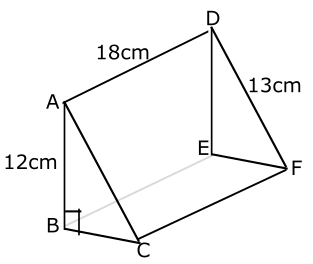
Calculate the volume of the regular three dimensional figure drawn above, where < ABC = 90° (a right- angled triangle).
- A. 394 cm\(^3\)
- B. 425 cm\(^3\)
- C. 268 cm\(^3\)
- D. 540 cm\(^3\)
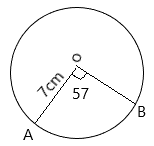
In the circle above, with centre O and radius 7 cm. Find the length of the arc AB, when < AOB = 57°.
- A. 5.32 cm
- B. 4.39 cm
- C. 7.33 cm
- D. 6.97 cm
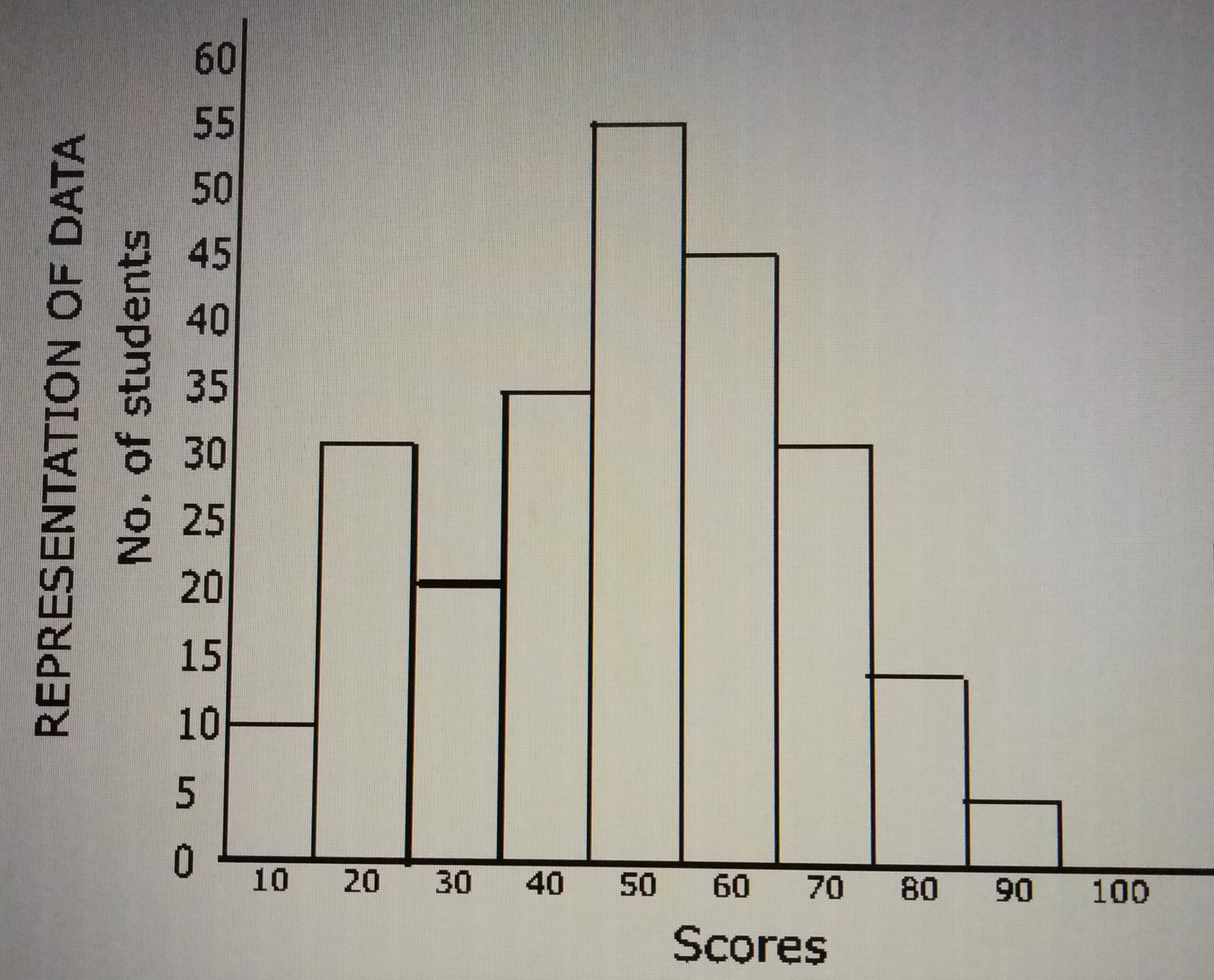
The histogram above represents the number of candidates who did Further Mathematics examination in a school. How many candidates scored more than 40?
- A. 100
- B. 79
- C. 150
- D. 90
| Marks | 1 | 2 | 3 | 4 | 5 |
| Frequency | 2y – 2 | y – 1 | 3y – 4 | 3 – y | 6 – 2y |
The table above is the distribution of data with mean equals to 3. Find the value of y.
- A. 5
- B. 2
- C. 3
- D. 6
Find the equation of a line perpendicular to the line 4y = 7x + 3 which passes through (-3, 1)
- A. 7y + 4x + 5 = 0
- B. 7y - 4x - 5 = 0
- C. 3y - 5x + 2 = 0
- D. 3y + 5x - 2 = 0
Find the distance between the points C(2, 2) and D(5, 6).
- A. 13 units
- B. 7 units
- C. 12 units
- D. 5 units
Differentiate \(\frac{2x}{\sin x}\) with respect to x.
- A. \(2 \cot x \sec x (1 + \tan x)\)
- B. \(2 \csc x - x \cot x\)
- C. \(2x \csc x + \tan x\)
- D. \(2\csc x(1 - x\cot x)\)


