A chord of a circle subtends an angle of 120° at the centre of a circle of diameter \(4\sqrt{3} cm\). Calculate the area of the major sector.
- A. 32\(\pi\) cm\(^2\)
- B. 4\(\pi\) cm\(^2\)
- C. 8\(\pi\) cm\(^2\)
- D. 16\(\pi\) cm\(^2\)
Find the length of a chord which subtends an angle of 90° at the centre of a circle whose radius is 8 cm.
- A. \(8\sqrt{3}\) cm
- B. 4 cm
- C. 8 cm
- D. \(8\sqrt{2}\) cm
A square tile has side 30 cm. How many of these tiles will cover a rectangular floor of length 7.2m and width 4.2m?
- A. 720
- B. 336
- C. 420
- D. 576
If the angles of a quadrilateral are (3y + 10)°, (2y + 30)°, (y + 20)° and 4y°. Find the value of y.
- A. 66°
- B. 12°
- C. 30°
- D. 42°
Find \(\frac{\mathrm d y}{\mathrm d x}\) if \(y = \cos x\).
- A. \(\sin x\)
- B. \(- \sin x\)
- C. \(\tan x\)
- D. \(- \tan x\)
A man stands on a tree 150 cm high and sees a boat at an angle of depression of 74°. Find the distance of the boat from the base of the tree.
- A. 52 cm
- B. 43 cm
- C. 40 cm
- D. 15 cm
A circular arc subtends angle 150° at the centre of a circle of radius 12cm. Calculate the area of the sector of the arc.
- A. 30\(\pi\) cm\(^2\)
- B. 60\(\pi\) cm\(^2\)
- C. 120\(\pi\) cm\(^2\)
- D. 150\(\pi\) cm\(^2\)
If \(N = \begin{pmatrix} 3 & 5 & -4 \\ 6 & -3 & -5 \\ -2 & 2 & 1 \end{pmatrix}\), find \(|N|\).
- A. 65
- B. 23
- C. 17
- D. 91
If X, Y can take values from the set (1, 2, 3 ,4), find the probability that the product of X and Y is not greater than 6
- A. \(\frac{5}{8}\)
- B. \(\frac{5}{16}\)
- C. \(\frac{1}{2}\)
- D. \(\frac{3}{8}\)
Solve \(5^{2(x – 1)} \times 5^{x + 1} = 0.04\)
- A. \(\frac{1}{3}\)
- B. \(\frac{1}{4}\)
- C. \(-\frac{1}{5}\)
- D. \(-\frac{1}{3}\)
Subtract 16418\(_9\) from 18630\(_9\).
- A. 1121\(_9\)
- B. 2112\(_9\)
- C. 2113\(_9\)
- D. 2211\(_9\)
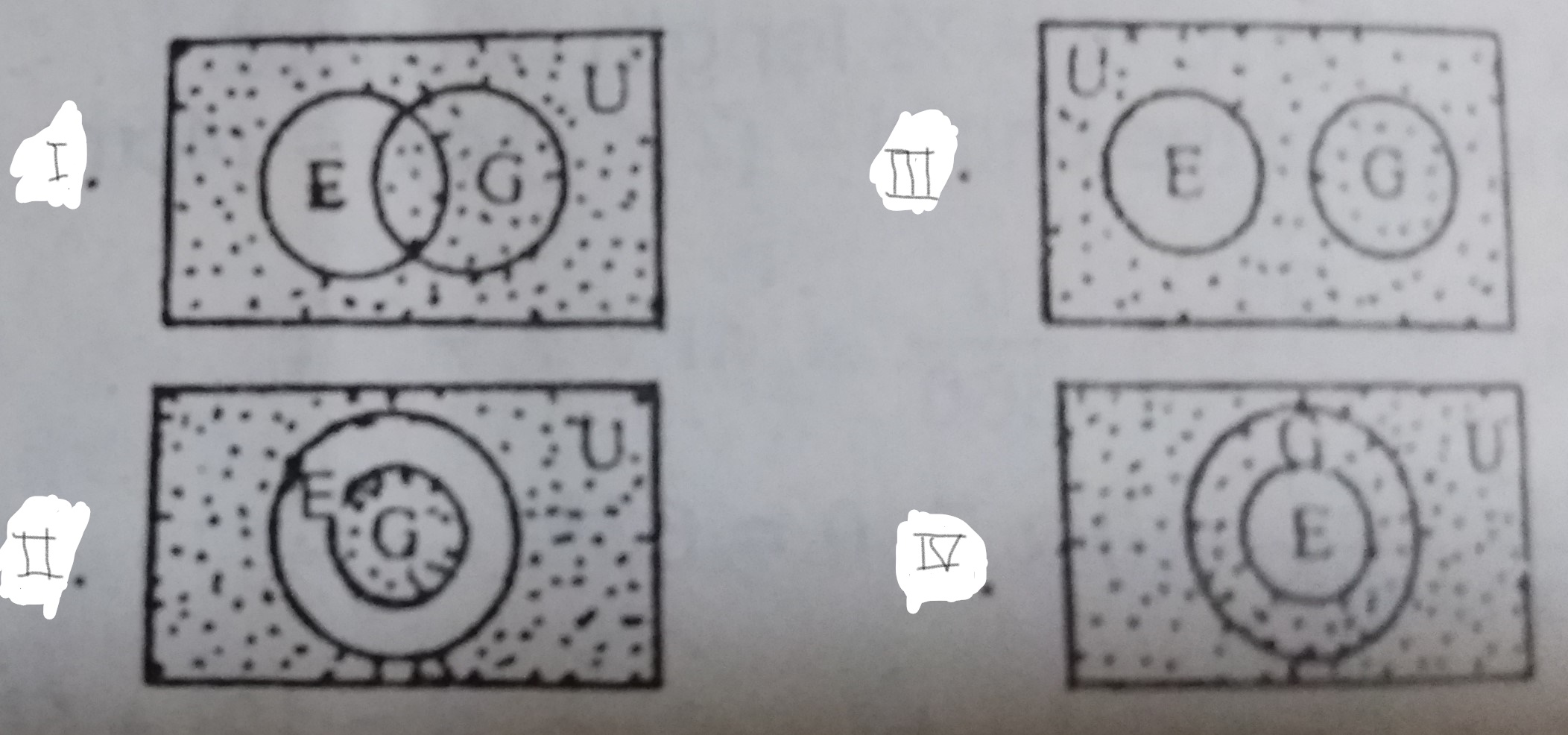
If \(E \subseteq G \subseteq U\), where U is the universal set, then the shaded venn diagram representing \(U – E\) or \(E^{c}\) is
- A. I
- B. II
- C. III
- D. IV
The table below shows the frequency distribution of the marks of 800 candidates in an examination.
| Marks | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Freq | 10 | 40 | 80 | 140 | 170 | 130 | 100 | 70 | 40 | 20 |
(a) (i) Construct a cumulative frequency table ; (ii) Draw the Ogive ; (iii) Use your ogive to determine the 50th percentile.
(b) The candidates that scored less than 25% are to be withdrawn from the institution, while those that scored than 75% are to be awarded scholarship. Estimate the number of students that will be retained, but will not enjoy the award.
Using a ruler and a pair of compasses only,
(a) construct (i) a triangle ABC such that |AB| = 5cm, |AC| = 7.5cm and < CAB = 120° ; (ii) the locus \(L_{1}\) of points equidistant from A and B ; (iii) the locus \(L_{2}\) of points equidistant from Ab and AC, which passes through the triangle ABC.
(b) Label the point P where \(L_{1}\) and \(L_{2}\) intersect;
(c) Measure |CP|.
(a) Prove that the sum of the angles in a triangle is two right angles.
(b) In a triangle LMN, the side NM is produced to P and the bisector of < LNP meets ML produced at Q. If < LMN = 46°, and < MLN = 80°, calculate < LQN, stating clearly your reasins.
Two towns K and Q are on the parallel of latitude 46°N. The longitude of town K is 130°W and that of town Q is 103°W. A third town P also on latitude 46°N is on longitude 23°E, Calculate:
(i) the length of the parallel of latitude 46°N, to the nearest 100km;
(ii) the distance between K and Q, correct to the nearest 100km;
(iii) the distance between Q and P measured along the parallel of latitude, to the nearest 10km.
[Take \(\pi = 3.142\); Radius of the earth = 6400km]
The table below is for the relation \(y = 2 + x – x^{2}\)
| x | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| y | -4 | -1.75 | 0 | 1.25 | 2 | 2.25 | 2 | 1.25 | 0 | -1.75 | -4 |
(a) Using a scale of 2cm to 1 unit on each axis, draw the graph of the relation in the interval \(-2 \leq x \leq 3\).
(b) From your graph, find the greatest value of y and the value of x for which this occurs.
(c) Using the same scale and axes, draw the graph of \(y = 1 – x\)
(d) Use your graphs to solve the equation \(1 + 2x – x^{2} = 0\)
Illustrate the following on graph paper and shade the region which satisfies all the three inequalities at the same time :
\(- x + 5y \leq 10 ; 3x – 4y \leq 8\) and \(x > -1\).
(a) The subsets A, B and C of a universal set are defined as follows :
A = {m, a, p, e} ; B = {a, e, i, o, u} ; C = {l, m, n, o, p, q, r, s, t, u}. List the elements of the following sets.
(i) \(A \cup B\) ; (ii) \(A \cup C\) ; (iii) \(A \cup (B \cap C)\).
(b) Out of the 400 students in the final year in a Senior Secondary School, 300 are offering Biology and 190 are offering Chemistry.
(i) How many students are offering both Biology and Chemistry, if only 70 students are offering neither Biology nor Chemistry? (ii) How many students are offering at least one of Biology or Chemistry?
A sector of a circle of radius 7cm subtending an angle of 270° at the centre of the circle is used to form a cone.
(a) Find the base radius of the cone.
(b) Calculate the area of the base of the cone to the nearest square centimetre.
[Take \(\pi = \frac{22}{7}\)]
In a certain school, the lesson periods for each week are as itemised below: English 10, Mathematics 7, Biology 3, Statistics 4, Ibo 3, others 9. Draw a pie chart to illustrate this information.


