(a) Copy and complete the following table for the relation \(y = \frac{5}{2} + x – 4x^{2}\)
| x | -2.0 | -1.5 | -1.0 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2.0 |
| y | -15.5 | 1 | 2.5 |
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, draw the graph of the relation for \(-2.0 \leq x \leq 2.0\).
(c) What is the maximum value of y?
(d) From your graph, obtain the roots of the equation \(8x^{2} – 2x – 5 = 0\)
(a) 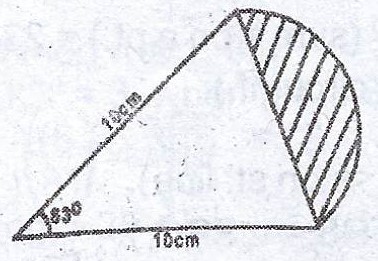
Calculate the area of the shaded segment of the circle shown in the diagram [Take \(\pi = \frac{22}{7}\)]
(b) A tin has radius 3cm and height 6cm. Find the (i) total surface area of the tin ; (ii) volume, in litres, that will fill the tin to capacity, correct to two decimal places.
[Take \(\pi = \frac{22}{7}\)]
(a) Using a ruler and a pair of compasses only, construct: (i) a triangle ABC such that |AB| = 5cm, |AC| = 7.5cm and < CAB = 120°; (ii) the locus \(l_{1}\) of points equidistant from A and B; (iii) the locus \(l_{2}\) of points equidistant from AB and AC which passes through triangle ABC .
(b) Label the point P where \(l_{1}\) and \(l_{2}\) intersect.
(c) Measure |CP|.
(a) If \(17x = 375^{2} – 356^{2}\), find the exact value of x.
(b) If \(4^{x} = 2^{\frac{1}{2}} \times 8\), find x.
(c) The sum of the first 9 terms of an A.P is 72 and the sum of the next 4 terms is 71, find the A.P.
(a) In a game, a fair die is rolled once and two unbiased coins are tossed at once. What is the probability of obtaining 3 and a tail?
(b) A box contains 10 marbles, 7 of which are black and 3 are red. Two marbles are drawn one after the other without replacement. Find the probability of getting:
(i) a red, then a black marble ; (ii) two black marbles.
(a) The sides PQ and PR of \(\Delta\) PQR are produced to T and S respectively, such that TQR = 131° and < QRS = 98°. Find < QPR.
(b) The circumference of a circular track is 400m. Find its radius, correct to the nearest metre. [Take \(\pi = \frac{22}{7}\)]
(a) The angle of a sector of a circle radius 7cm is 108°. Calculate the perimeter of the sector. [Take \(\pi = \frac{22}{7}\)]
(b) A boat is on the same horizontal level as the foot of a cliff, and the angle of depression of the boat from the top of the cliff is 30°. If the boat is 120m away from the foot of the cliff, find the height of the cliff correct to three significant figures.
(a) Solve the following pair of simultaneous equations: \(2x + 5y = 6\frac{1}{2} ; 5x – 2y = 9\)
(b) If \(\log_{10} (2x + 1) – \log_{10} (3x – 2) = 1\), find x.
(a) If \(9^{2x – 1} = \frac{81^{x – 2}}{3^{x}}\), find x.
(b) Without using Mathematical Tables, evaluate: \(\sqrt{\frac{0.81 \times 10^{-5}}{2.25 \times 10^{7}}}\)
P and Q are two points on latitude 55°N and their longitudes are 33°W and 20°E respectively. Calculate the distance between P and Q measured along
(a) the parallel of latitude ;
(b) a great circle.
[Take \(\pi = \frac{22}{7}\) and radius of the earth = 6400km].
The table below shows the frequency distribution of the marks scored by fifty students in an examination.
| Marks (%) | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Freq | 2 | 3 | 4 | 6 | 13 | 10 | 5 | 3 | 2 | 2 |
(a) Draw the cumulative frequency curve for the distribution.
(b) Use your curve to estimate the : (i) upper quartile; (ii) pass mark if 60% of the students passed.
(a) Copy and complete the following table of values for \(y = 3\sin 2\theta – \cos \theta\).
| \(\theta\) | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| y | -1.0 | 0 | 1.0 |
(b) Using a scale of 2cm to 30° on the \(\theta\) axis and 2cm to 1 unit on the y- axis, draw the graph of \(y = 3 \sin 2\theta – \cos \theta\) for \(0° \leq \theta \leq 180°\).
(c) Use your graph to find the : (i) solution of the equation \(3 \sin 2\theta – \cos \theta = 0\), correct to the nearest degree; (ii) maximum value of y, correct to one decimal place.
(a) What is the 25th term of 5, 9, 13,… ?
(b) Find the 5th term of \(\frac{8}{9}, \frac{-4}{3}, 2, …\).
(c) The 3rd and 6th terms of a G.P are \(48\) and \(14\frac{2}{9}\) respectively. Write down the first four terms of the G.P.
(a) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.
(b) 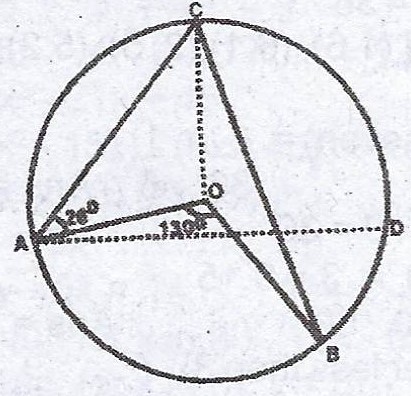
In the diagram, O is the centre of the circle ACDB. If < CAO = 26° and < AOB = 130°. Calculate : (i) < OBC ; (ii) < COB.
(a) 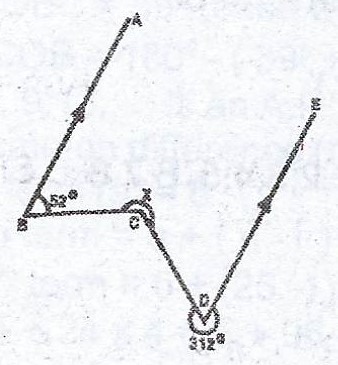
In the diagram, BA is parallel to DE. Find the value of x.
(b) Illustrate graphically and shade the region in which inequalities \(y – 2x < 5 ; 2y + x \geq 4 ; y + 2x \leq 10\) are satisfied.
(a)(i) Given that \(\log_{10} 5 = 0.699\) and \(\log_{10} 3 = 0.477\), find \(\log_{10} 45\), without using Mathematical tables.
(ii) Hence, solve \(x^{0.8265} = 45\).
(b) Use Mathematical tables to evaluate \(\sqrt{\frac{2.067}{0.0348 \times 0.538}}\)
A box contains identical balls of which 12 are red, 16 white and 8 blue. Three balls are drawn from the box one after the other without replacement. Find the probability that :
(a) three are red;
(b) the first is blue and the other two are red;
(c) two are white and one is blue.
(a) Simplify \(\frac{3}{m + 2n} – \frac{2}{m – 3n}\)
(b) A number is made up of two digits. The sum of the digits is 11. If the digits are interchanged, the original number is increased by 9. Find the number.
A simple measuring device is used at points X and Y on the same horizontal level to measure the angles of elevation of the peak P of a certain mountain. If X is known to 5,200m above sea level, /XY/ = 4,000m and the measurements of the angles of elevation of P at X and Y are 15° and 35° respectively, find the height of the mountain. (Take \(\tan 15 = 0.3\) and \(\tan 35 = 0.7\))
The universal set \(\varepsilon\) is the set of all integers and the subset P, Q, R of \(\varepsilon\) are given by:
\(P = {x : x < 0} ; Q = {… , -5, -3, -1, 1, 3, 5} ; R = {x : -2 \leq x < 7}\)
(a) Find \(Q \cap R\).
(b) Find \(R’\) where R’ is the complement of R with respect to \(\varepsilon\).
(c) Find \(P’ \cup R’\)
(d) List the members of \((P \cap Q)’\).
(a) Simplify, without using Mathematical tables: \(\log_{10} (\frac{30}{16}) – 2 \log_{10} (\frac{5}{9}) + \log_{10} (\frac{400}{243})\)
(b) Without using Mathematical tables, calculate \(\sqrt{\frac{P}{Q}}\) where \(P = 3.6 \times 10^{-3}\) and \(Q = 2.25 \times 10^{6}\), leaving your answer in standard form.

