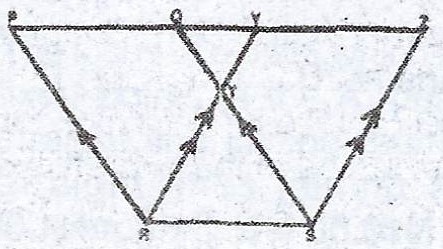
(a) In the diagram, PQSR and SRYZ are parallelograms and PQYZ is a straight line. If /QY/ = 2cm and /RS/ = 3cm, find /PZ/.
(b) P and Q are two towns on the earth’s surface on latitude 56°N. Thei longitudes are 25°E and 95°E respectively. Find the distance PQ along their parallel of latitude, correct to the nearest km. [Take radius of the earth as 6400km and \(\pi = \frac{22}{7}\)]
The quantity y is partly constant and partly varies inversely as the square of x.
(a) Write down the relationship between x and y.
(b) When x = 1, y = 11 and when x = 2, y = 5, find the value of y when x = 4.
(a) Factorise : \(px – 2px – 4qy + 2py\)
(b) Given that the universal set U = {1, 2, 3, 4,5, 6, 7, 8, 9, 10}, P = {1, 2, 4, 6, 10} and Q = {2, 3, 6, 9}; show that \((P \cup Q)’ = P’ \cap Q’\)
Two men P and Q set off from a base camp R, prospecting for oil. P moves 20km on a bearing of 205° and Q moves 15km on a bearing of 060°. Calculate the:
(a) distance of Q from P ;
(b) bearing of Q from P.
(Give your answer in each case to the nearest whole number)
(a) P and Q are points on the parallel of latitude 68.7°S, their longitudes being 124°W and 56°E respectively. What is their distance apart measured along the parallel of latitude? [Take R = 6400km, \(\pi = 3.142\)]. (Give your answers to 3 significant figures).
(b) A bag contains four red, three white and five green balls. (i) If one ball is picked at random, what is the probability that it is not green? (ii) if two balls are picked at random without replacement, what is the probability that one is red and the other white?
(a) Make d the subject of the formula \(S = \frac{n}{2}[2a + (n – 1) d]\).
(b) (i)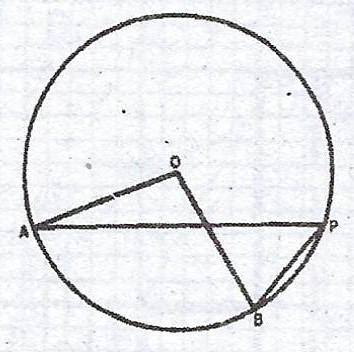 
In the diagram, O is the centre of the circle, A, B and P are points on the circumference. Prove that < AOB = 2 < APB.
(ii) 
Find the angles x, v and z in the diagram.
(a) Copy and complete the table for \(y = 3x^{2} – 5x – 7\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| \(y = 3x^{2} – 5x – 7\) | 35 | -7 | -9 | 5 |
(b) Using a scale of 2cm = 1 unit along the x- axis and 2cm = 5 units along the y- axis, draw the graph of \(y = 3x^{2} – 5x – 7\).
(c) On the same axis, draw the graph of \(y + 3x + 2 = 0\).
(d) From your graph, find the : (i) range of values of x for which \(3x^{2} – 5x – 7 < 0\) ; (ii) roots of the equation \(3x^{2} – 2x – 5 = 0\).
(a) Find the number N such that when \(\frac{1}{3}\) of it is added to 8, the result is the same as when \(\frac{1}{2}\) of it is subtracted from 18.
(b) Using a ruler and a pair of compasses only, construct a trapezium ABCD, in which the parallel sides AB and DC are 4 cm apart. < DAB = 60°, /AB/ = 8 cm and /BC/ = 5 cm. Measure /DC/.
(a) The universal set U is the set of integers, P, Q and R are subsets of U defined as follows:
\(P = x : x \leq 2 \) ; \(Q = x : -7 < x < 15\) ; \(R = x : -2 \leq x < 19\).
Find (i) \(P \cap Q\) ; (ii) \(P \cap (Q \cup R’)\), where R’ is the complement of R with respect to U.
(b) The following data shows the marks of 40 students in a History examination.
41 52 37 56 63 48 65 46 54 32 51 66 74 23 35 61 58 44 49 53 45 57 56 38 59 28 50 49 67 56 36 45 79 68 43 56 26 47 55 71.
(i) Form a grouped frequency table with the class intervals 20 – 29, 30 – 39, 40 – 49 etc; (ii) Find the mean of the distribution.
(a) Without using tables, find the value of \(\frac{0.45 \times 0.91}{0.0117}\)
(b) Find the number which is exactly halfway between \(1\frac{6}{7}\) and \(2\frac{11}{28}\).
(c) If each interior angle of a regular polygon is five times the exterior angle, how many sides has the polygon?
(d) Calculate the volume of the material used in making a pipe 20cm long, with an internal diameter 6cm and external diameter 8cm. [Take \(pi = \frac{22}{7}\)].
(a) ABCD is a trapezium with AB parallel to DC and /AD/ = /AB/. If < BAD = 106°, find < BDC.
(b) The table below shows the distribution of 20 cards labelled A – E.
| Card | A | B | C | D | E |
| Frequency | 3 | 4 | 7 | 5 | 1 |
(i) If a card is selected at random from the pack, what is the probability that the card is E? (ii) If two cards are selected at random one after the other without replacement from the pack, what is the probability that one of the two cards is B?
(a) If \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), calculate without using tables, the value of \(\log_{10} 0.72\).
(b) A hawk on top of a tree, 20 metres high views a chick on the ground at an angle of depression of 39°. Find, correct to 2 significant figures, the distance of the chick from the bottom of the tree.
The table below shows the marks obtained by forty pupils in a Mathematics test.
| Marks | 0 – 9 | 10 – 19 | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 |
| No of pupils | 4 | 5 | 6 | 12 | 8 | 5 |
(a) Draw a histogram for the mark distribution ;
(b) Use your histogram to estimate the mode ;
(c) Calculate the median of the distribution.
(a) Solve the simultaneous equation : \(6y + 5x = 12 ; 4y – 3x = 11\).
(b)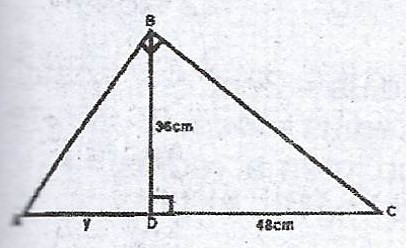 
In the diagram, ADC is a straight line. /CD/ = 48 cm, /BD/ = 36 cm and /AD/ = y cm. Find the value of y.
A shopkeeper buys 40 kg of fruits for N120.00. He sells 20 kg at N5.00 per kg, 10 kg at N3.00 per kg, 5 kg at N2.00 per kg and the remaining 5 kg at 50k per kg. Calculate the :
(a) amount he realises from the sales ;
(b) total profit / loss ;
(c) percentage profit/ loss on his outlay of N120.00.
The table below shows the mark distribution of candidates in an aptitude test for selection into the public service.
| Marks (in %) | Freq |
| 44 – 46 | 2 |
| 47 – 49 | 5 |
| 50 – 52 | 11 |
| 53 – 55 | 20 |
| 56 – 61 | 42 |
| 62 – 64 | 46 |
| 65 – 67 | 36 |
| 68 – 70 | 9 |
| 71 – 73 | 3 |
(a) Make a cumulative frequency for the distribution
(b) Draw the cumulative frequency curve.
(c) From your graph, estimate the median mark.
(d) The cut-off mark was 63%. What percentage of the candidates was selected?
(a)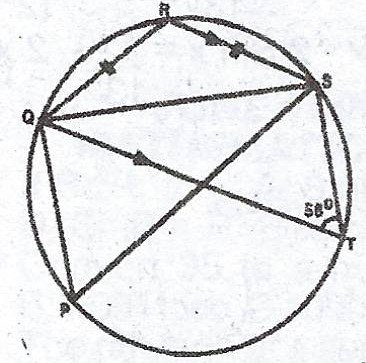 
PQRST is a circle with centre C. PCS is a straight line, RS // QT, |QR| = |RS| and < QTS = 56°. Find (i) SQT (ii) PQT.
(b)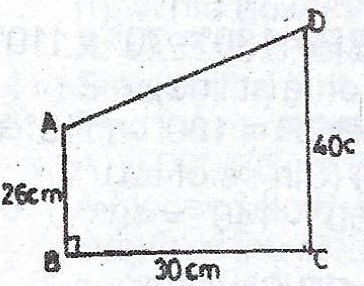 
In the diagram, points B and C are on a horizontal plane and |BC| = 30cm. A and D are points vertically above B and C respectively. |DC| = 40 cm and |AB| = 26 cm. Calculate the angles of depression of : (i) B from D ; (ii) A from D ; correct to the nearest degree.
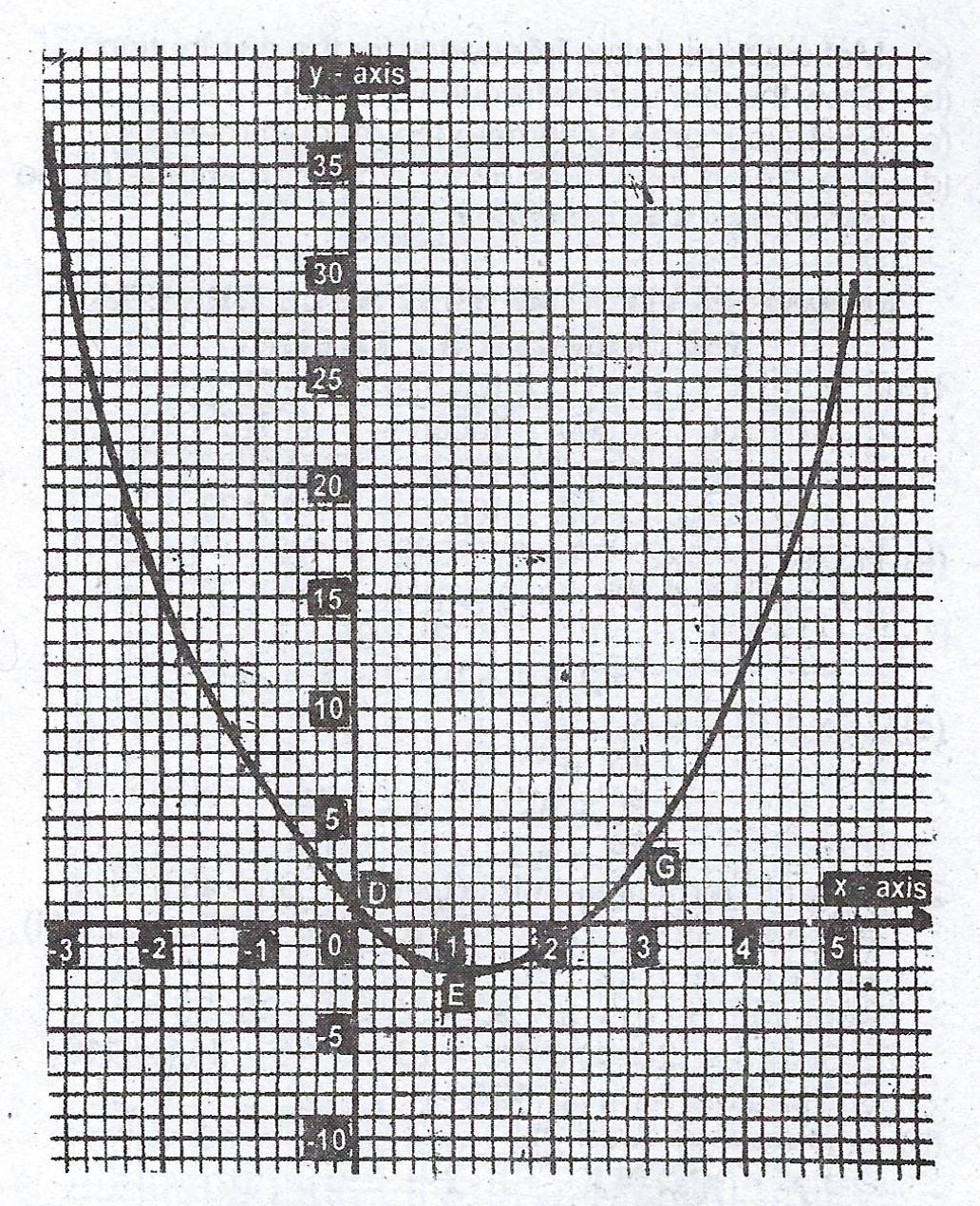
Above is the graph of the quadratic function \(y = ax^{2} + bx + c\) where a, b and c are constants. Using the graph, find :
(a)(i) the scales on both axes ; (ii) the equation of the line of symmetry of the curve ; (iii) the roots of the quadratic equation \(ax^{2} + bx + c = 0\)
(b) Use the coordinates of D, E and G to find the values of the constants a, b and c hence write down the quadratic function illustrated in the graph.
(c) Find the greatest value of y within the range \(-3 \leq x \leq 5\).
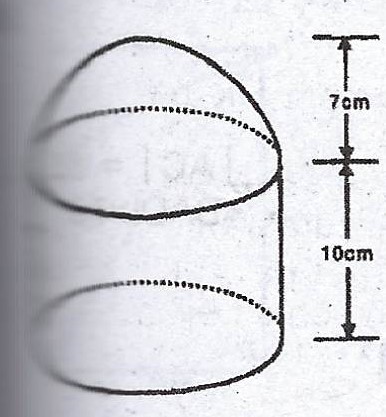The solid is a cylinder surmounted by a hemispherical bowl. Calculate its
(a) total surface area ;
(b) volume (Take \(\pi = \frac{22}{7}\))
(a) Solve the simultaneous equation : \(\log_{10} x + \log_{10} y = 4\)
\(\log_{10} x + 2\log_{10} y = 3\)
(b) The time, t, taken to buy fuel at a petrol station varies directly as the number of vehicles V on queue and jointly varies inversely as the number of pumps P available in the station. In a station with 5 pumps, it took 10 minutes to fuel 20 vehicles. Find :
(i) the relationship between t, P and V ; (ii) the time it will take to fuel 50 vehicles in the station with 2 pumps ; (iii) the number of pumps required to fuel 40 vehicles in 20 minutes.
(a) Using a ruler and a pair of compasses only, construst \(\Delta\) ABC in which |AB| = 7cm, |BC| = 5cm and < ABC = 75°. Measure |AC|.
(b) In (a) above, locate by construction, a point D such that CD is parallel to AB and D is equidistant from points A and C. Measure < BAD.