The cost of maintaining a school is partly constant and partly varies as the number of pupils. With 50 pupils, the cost is $15,705.00 and with 40 pupils, it is $13,305.00.
(a) Find the cost when there are 44 pupils.
(b) If the fee per pupil is $360.00, what is the least number of pupils for which the school can run without a loss?
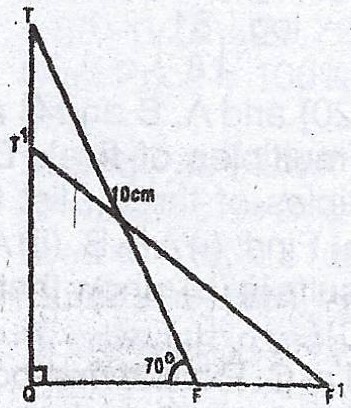
In the diagram, a ladder TF, 10 metres long is placed against a wall at an angle of 70° to the horizontal.
(a) How high up the wall, correct to the nearest metre, does the ladder reach?
(b) If the foot (F) of the ladder is pulled from the wall to F\(^{1}\) by 1 metre, (i) how far, correct to 2 significant figures, does the top T slide down the wall to T\(^{1}\).
(ii) Calculate, correct to the nearest degree, \(QF^{1}T^{1}\).
(a) Given that \(\sin(A + B) = \sin A \cos B + \cos A \sin B\). Without using mathematical tables or calculator, evaluate \(\sin 105°\), leaving your answer in the surd form.
(You may use 105° = 60° + 45°)
(b) The houses on one side of a particular street are assigned odd numbers, starting from 11. If the sum of the numbers is 551, how many houses are there?
(c) The 1st and 3rd terms of a Geometric Progression (G.P) are \(2\) and \(\frac{2}{9}\) respectively. Find :
(i) the common difference ; (ii) the 5th term.
(a) A cylindrical pipe is 28 metres long. Its internal radius is 3.5 cm and external radius 5 cm. Calaulate : (i) the volume, in cm\(^{3}\), of metal used in making the pipe ; (ii) the volume of water in litres that the pipe can hold when full, correct to 1 decimal place. [Take \(\pi = \frac{22}{7}\)]
(b)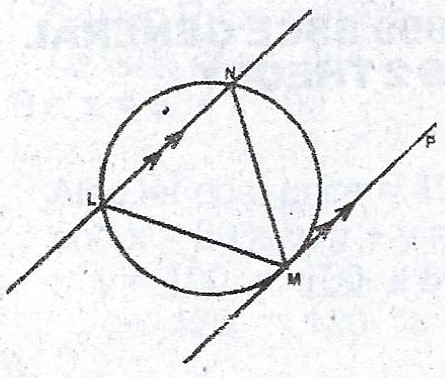 
In the diagram, MP is a tangent to the circle LMN at M. If the chord LN is parallel to MP, show that the triangle LMN is isosceles.
The table gives the frequency distribution of marks obtained by a group of students in a test.
| Marks | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequency | 5 | x – 1 | x | 9 | 4 | 1 |
If the mean is 5,
(a) Calculate the value of x;
(b) Find the : (i) mode ; (ii) median of the distribution.
(c) If one of the students is selected at random, find the probability that he scored at least 7 marks.
(a) Solve the simultaneous equations 3y – 2x = 21 ; 4y + 5x = 5.
(b) Six identical cards numbered 1 – 6 are placed face down. A card is to be picked at random. A person wins $60.00 if he picks the card numbered 6. If he picks any of the other cards, he loses $10.00 times the number on the card. Calculate the probability of (i) losing ; (ii) losing $20.00 after two picks.
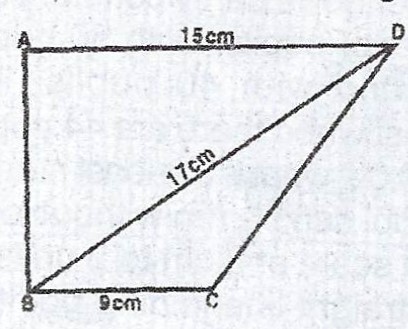
In the diagram, ABCD is a trapezium in which \(AD \parallel BC\) and \(< ABC\) is a right angle. If |AD| = 15 cm, |BD| = 17 cm and |BC| = 9 cm, calculate :
(a) |AB| ;
(b) the area of the triangle BCD ;
(c) |CD| ;
(d) perimeter of the trapezium.
ABC is a triangle, right-angled at C. P is the mid-point of AC, < PBC = 37° and |BC| = 5 cm. Calculate :
(a) |AC|, correct to 3 significant figures ;
(b) < PBA.
(a) If \(\varepsilon\) is the set \({1, 2, 3,…, 19, 20}\) and A, B and C are subsets of \(\varepsilon\) such that A = { multiples of five}, B = {multiples of four} and C = {multiples of three}, list the elements of (i) A ; (ii) B ; (iii) C ;
(b) Find : (i) \(A \cap B\) ; (ii) \(A \cap C\) ; (iii) \(B \cup C\).
(c) Using your results in (b), show that \((A \cap B) \cup (A \cap C) = A \cap (B \cup C)\).
(a) Simplify \((\frac{4}{25})^{-\frac{1}{2}} \times 2^{4} \div (\frac{15}{2})^{-2}\)
(b) Evaluate \(\log_{5} (\frac{3}{5}) + 3 \log_{5} (\frac{5}{2}) – \log_{5} (\frac{81}{8})\).
(a) Two places X and Y on the equator are on longitudes 67°E and 123°E respectively. (i) What is the distance between them along the equator? (ii) How far from the North pole is X? [Take \(\pi = \frac{22}{7}\) and radius of earth = 6400km].
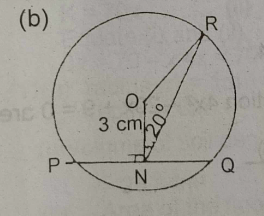
(b) SEE FIGURE B above, In the diagram, PQR is a circle centre O. N is the mid-point of chord PQ. |PQ| = 8cm, |ON| = 3cm and < ONR = 20°. Calculate the size of < ORN to the nearest degree.
(a) The first term of an Arithmetic Progression (A.P) is 8. The ratio of the 7th term to the 9th term is 5 : 8. Calculate the common difference of the progression.
(b) A sphere of radius 2 cm is of mass 11.2g. Find (i) the volume of the sphere ; (ii) the density of the sphere ; (iii) the mass of a sphere of the same material but with radius 3cm. [Take \(\pi = \frac{22}{7}\)].
(a) A cylindrical well of radius 1 metre is dug out to a depth of 8 metres. (i) calculate, in m\(^{3}\), the volume of soil dug out ; (ii) if the soil is used to raise the level of rectangular floor of a room 4m by 12m, calculate, correct to the nearest cm, the thickness of the new layer of soil. [Take \(\pi = \frac{22}{7}\)].
(b) see figure b above.
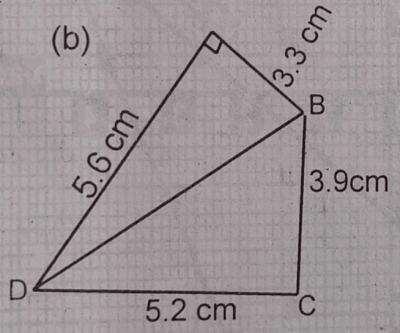
The diagram shows a quadrilateral ABCD in which < DAB is a right-angle. |AB| = 3.3 cm, |BC| = 3.9 cm, |CD| = 5.6 cm. (i) find the length of BD. (ii) show that < BCD = 90°.
(a) A surveyor walks 100m up a hill which slopes at an angle of 24° to the horizontal. Calculate, correct to the nearest metre, the height through which he rises.
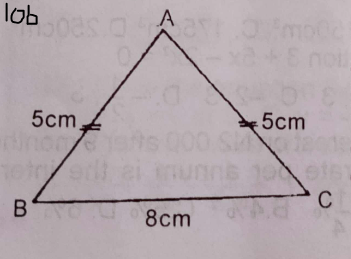
(b) Use Figure 10b above to answer the question below.
In the diagram, ABC is an isosceles triangle. |AB| = |AC| = 5 cm, and |BC| = 8 cm. Calculate, correct to the nearest degree, < BAC.
(c) Two boats, 70 metres apart and on opposite sides of a light-house, are in a straight line with the light-house. The angles of elevation of the top of the light-house from the two boats are 71.6° and 45°. Find the height of the light-house. [Take tan 71.6° = 3].
(a) The mean of 1, 2, x, 11, y, 14, arranged in ascending order, is 8 and the median is 9. Find the values of x and y.
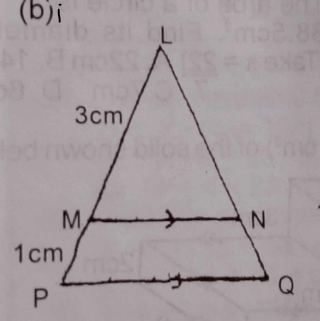
(b) Use the figure above to answer the question(i) below.
(i) In the diagram, MN || PQ, |LM| = 3cm and |LP| = 4cm. If the area of \(\Delta\) LMN is 18\(cm^{2}\), find the area of the quadrilateral MPQN.
(a) Copy and complete the following table of values for the relation \(y = x^{2} – 2x – 5\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -2 | -6 | -2 | 3 | 10 |
(b) Draw the graph of the relation \(y = x^{2} – 2x – 5\); using a scale of 2 cm to 1 unit on the x- axis, and 2 cm to 2 units on the y- axis.
(c) Using the same axes, draw the graph of \(y = 2x + 3\).
(d) Obtain in the form \(ax^{2} + bx + c = 0\) where a, b and c are integers, the equation which is satisfied by the x- coordinate of the points of intersection of the two graphs.
(e) From your graphs, determine the roots of the equation obtained in (d) above.
(a) A man earns N150,000 per annum. He is allowed a tax free pay on N40,000. If he pays 25 kobo in the naira as tax on his taxable income, how much has he left?
(b) A bookshop has 650 copies of a book for sale. The books were marked at N75 per copy in order to make a profit of 30%. A bookseller bought 300 copies at 5% discount. If the remaining copies are sold at N75 each, calculate the percentage profit the bookshop would make on the whole.
(a)
| Limes | Apples | |
| Good | 10 | 8 |
| Bad | 6 | 6 |
The table shows the number of limes and apples of the same size in a bag. If two of the fruits are picked at random, one at a time, without replacement, find the probability that : (i) both are good limes ; (ii) both are bad fruits ; (iii) one is a good apple and the other a bad lime.
(b) Solve the equation \(\log_{3} (4x + 1) – \log_{3} (3x – 5) = 2\).
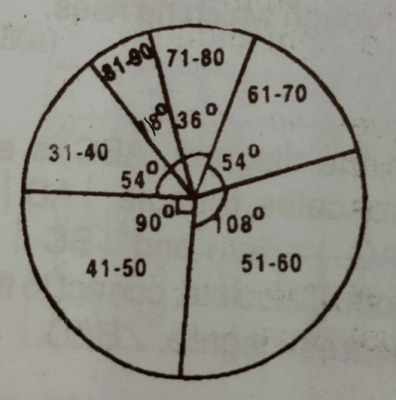
The pie chart above shows the distribution of marks scored by 200 pupils in a test.
(a) How many pupils scored : (i) between 41 and 50 marks? ; (ii) above 80 marks?
(b) What fraction of the pupils scored at most 50 marks?
(c) What is the modal class?
Using ruler and a pair of compasses only,
(a) construct \(\Delta PQR\) such that |PQ| = 7 cm, |PR| = 6 cm and < PQR = 60°.
(b) locate point M, the mid-point of PQ.
(c) Measure < RMQ.
(a) Given the expression \(y = ax^{2} – bx – 12\) , find the values of x when a = 1, b = 2 and y = 3.
(b) If \(\sqrt{x^{2} + 1} = \frac{5}{4}\), find the positive value of x.