(a) Given that cos x = 0.7431, 0° < x < 90°, use tables to find the values of : (i) 2sin x ; (ii) tan\(\frac{x}{2}\).
(b) The interior angles of a pentagon are in ratio 2 : 3: 4: 4: 5. Find the value of the largest angle.
(a) Evaluate and express your answer in standard form : \(\frac{4.56 \times 3.6}{0.12}\)
(b) Without using mathematical tables or calculator, evaluate \((73.8)^{2} – (26.2)^{2}\).
(c) Simplify \(\sqrt{1\frac{19}{81}}\), expressing your answer in the form \(\frac{a}{b}\) where a and b are positive integers.
(a) A boy blew his rubber balloon to a spherical shape. The balloon burst when its diameter was 15 cm. Calculate, correct to the nearest whole number, the volume of air in the balloon at the point of bursting. [Take \(\pi = \frac{22}{7}\)]
(b) A point X is on latitude 28°N and longitude 105°W. Y is another point on the same latitude as X but on longitude 35°E. (i) Calculate, correct to three significant figures, the distance between X and Y along latitude 28°N ; (ii) How far is X from the equator? [Take \(\pi = \frac{22}{7}\) and radius of the earth = 6,400km].
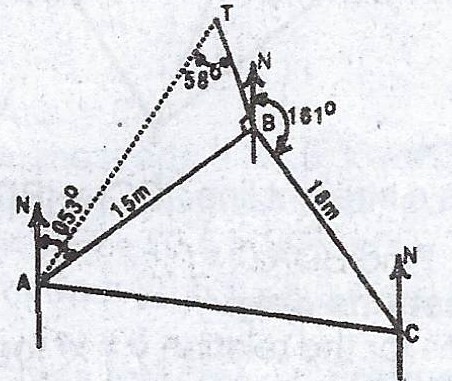In the diagram, three points A, B and C are on the same horizontal ground. B is 15m from A, on a bearing of 053°, C is 18m from B on a bearing of 161°. A vertical pole with top T is erected at B such that < ATB = 58°. Calculate, correct to three significant figures,
(a) the length of AC.
(b) the bearing of C from A ;
(c) the height of the pole BT.
(a) The roots of the equation \(2x^{2} + (p + 1)x + 9 = 0\), are 1 and 3, where p and q are constants. Find the values of p and q.
(b) The weight of an object varies inversely as the square of its distance from the centre of the earth. A small satellite weighs 80kg on the earth’s surface. Calculate, correct to the nearest whole number, the weight of the satellite when it is 800km above the surface of the earth. [Take the radius of the earth as 6,400km].
(a) The probabilities that three boys pass an examination are \(\frac{2}{3}, \frac{5}{8}\) and \(\frac{3}{4}\) respectively. Find the probability that :
(i) all three boys pass ; (ii) none of the boys pass ; (iii) only two of the boys pass.
(b) A shop-keeper marks a television set for sale at N36,000 so as to make a profit of 20% on the cost price. When he sells it, he allows a discount of 5% of the marked price. Calculate the actual percentage profit.
(a) In a market survey, 100 traders sell fruits, 40 sell apples, 46 oranges, 50 mangoes, 14 apples and oranges, 15 apples and mangoes and 10 sell the three types of fruits. Each of the 100 traders sells at least one of the three fruits.
(i) Represent the information in a Venn diagram ; (ii) Find the number that sell oranges and mangoes only.
(b) Find the value of x for which \(312_{four} + 52_{x} = 96_{ten}\)
The number of child births recorded in 50 maternity centres of a local government in August 1993 are as follows :
50 99 81 86 69 85 93 63 92 65 77 74 76 71 90 74 81 94 67 75 95 81 68 105 99 68 75 75 76 73 79 74 80 69 74 62 74 80 79 68 79 75 75 71 83 75 80 85 81 82
(a) Construct a frequency distribution table, using class intervals 45 – 54, 55 – 64, etc.
(b) Draw the histogram for the distribution
(c) Use your histogram to estimate the mode.
(d) Calculate the mean number of births.
(a) Draw the table of values for the relation \(y = x^{2}\) for the interval \(-3 \leq x \leq 4\).
(b) Using a scale of 2 cm to 1 unit on the x- axis and 2 cm to 2 units on the y- axis, draw the graphs of : (i) \(y = x^{2}\) ; (ii) \(y = 2x + 3\) for \(-3 \leq x \leq 4\).
(c) Use your graph to find : (i) the roots of the equation \(x^{2} = 2x + 3\) ; (ii) the gradient of \(y = x^{2}\) at x = -2.
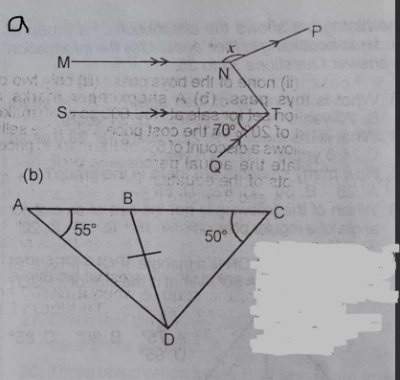
(a) see figure a above, In the diagram, MN || ST, NP || QT and < STQ = 70°. Find x.
(b) see figure b above, In the diagram above, AC is a straight line, |BC| = |BD|, \(\stackrel\frown{BCD} = 50°\) and \(\stackrel\frown{BAD} = 55°\). Find \(\stackrel\frown{BDA}\).
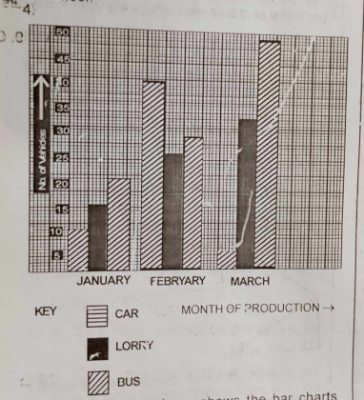
The diagram above shows the bar charts representing the number of vehicles manufactured by a company in January, February and March, 1992.
(a) How many vehicles were produced in February?
(b) What fraction of the vehicles manufactured in February were cars?
(c) How many buses were produced altogether from January to March, 1992?
(d) What is the ratio in the lowest term of the number of lorries produced in February to that in March?
The sides of a rectangular floor are xm and (x + 7)m. The diagonal is (x + 8)m. Calculate, in metres :
(a) the value of x ;
(b) the area of the floor.
(a) Simplify : \(\frac{1}{3^{5n}} \times 9^{n – 1} \times 27^{n + 1}\)
(b) The sum of the ages of a woman and her daughter is 46 years. In 4 years’ time, the ratio of their ages will be 7 : 2. Find their present ages.
Given that \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), calculate without using mathematical tables or calculator, the value of :
(a) \(\log_{10} 54\) ;
(b) \(\log_{10} 0.24\).
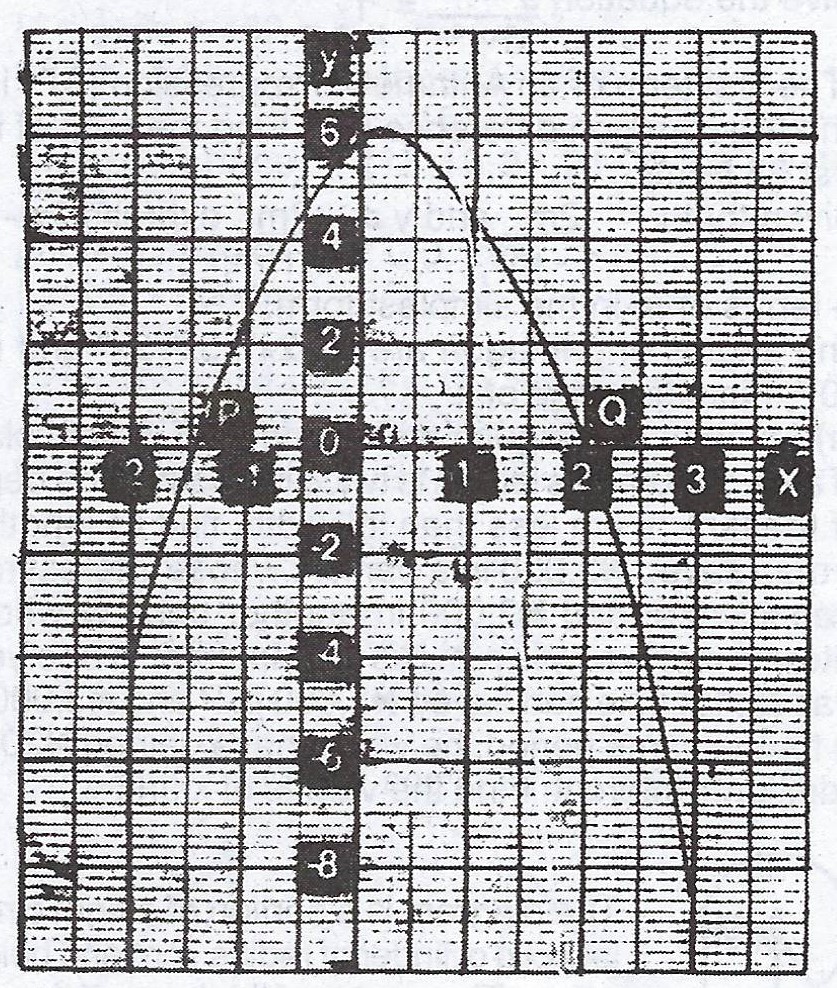
Given is the graph of the relation \(y = ax^{2} + bx + c\) where a, b and c are constants. Use the graph to :
(a) find the roots of the equation \(ax^{2} + bx + c = 0\);
(b) determine the values of constants a, b and c in the relation using the values of the coordinates P and Q and hence write down the relation illustrated in the graph
(c) find the maximum value of y and the corresponding value of x at this point.
(d) find the values of x when y = 2.
The following data gives the lengths, in cm, of 30 pieces of iron rods :
45 55 65 60 61 68 59 54 64 76 50 68 72 68 80 67 70 62 79 67 64 63 71 59 64 53 57 74 55 57
(a) Using class intervals of 45 – 49, 50 – 54, 55 – 59, … construct a frequency table of the data.
(b) Draw the histogram for the distribution
(c) Calculate the mean of the distribution
(d) What is the probability of selecting an iron rod whose length is in the modal class?
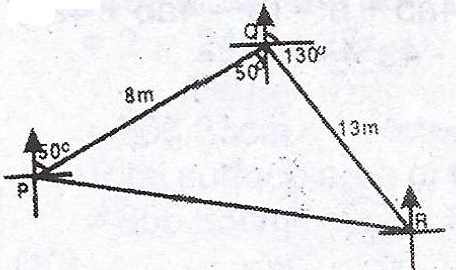In the diagram, /PQ/ = 8m, /QR/ = 13m, the bearing of Q from P is 050° and the bearing of R from Q is 130°.
(a) Calculate, correct to 3 significant figures, (i) /PR/ ; (ii) the bearing of R from P.
(b) Calculate the shortest distance between Q and PR, hence the area of triangle PQR.
Using ruler and a pair of compasses only,
(a) construct, (i) triangle XYZ with |XY| = 8cm, < YXZ = 60° and < XYZ = 30° ; (ii) the perpendicular ZT to meet XY in T ; (iii) the locus \(l_{1}\) of points equidistant from ZY and XY.
(b) If \(l_{1}\) and ZT intersect at S, measure |ST|.
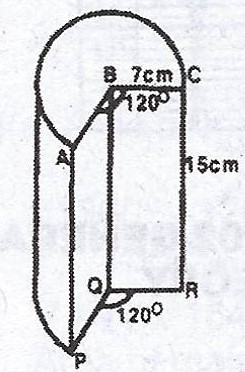The diagram is a portion of a right circular solid cylinder of radius 7 cm and height 15 cm. The centre of the base of the cylinder is Q, while that of the top is B, where \(\stackrel\frown{ABC} = \stackrel\frown{PQR} = 120°\). Calculate, correct to one decimal place:
(a) The volume
(b) the total surface area of the solid. [Take \(\pi = \frac{22}{7}\)].
(a) An open rectangular tank is made of a steel plate of area 1440\(m^{2}\). Its length is twice its width . If the depth of the tank is 4m less than its width, find its length.
(b) A man saved N3,000 in a bank P, whose interest rate was x% per annum and N2,000 in another bank Q whose interest rate was y% per annum. His total interest in one year was N640. If he had saved N2,000 in P and N3,000 in Q for the same period, he would have gained N20 as additional interest. Find the values of x and y.
(a) The first term of an Arithmetic Progression(AP) is 3 and the common difference is 4. Find the sum of the first 28 terms.
(b) Given that \(x = \frac{2m}{1 – m^{2}}\) and \(y = \frac{2m}{1 + m}\), express 2x – y in terms of m in the simplest form.
(c) The angles of pentagon are x°, 2x°, 3x°, 2x° and (3x – 10)°. Find the value of x.