(a) How many numbers between 75 and 500 are divisible by 7?
(b) The 8th term of an Arithmetic Progression (A.P) is 5 times the 3rd term while the 7th term is 9 greater than the 4th term. Write the first 5 terms of the A.P.
(a) Copy and complete the table of values for \(y = \sin x + 2 \cos x\), correct to one decimal place.
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° |
240° |
| y | 2.2 | -1.2 | -2.0 | -1.9 |
(b) Using a scale of 2 cm to 30° on the x- axis and 2 cm to 0.5 units on the y- axis, draw the graph of \(y = \sin x + 2\cos x\) for \(0° \leq x \leq 240°\).
(c) Use your graph to solve the equation : (i) \(\sin x + 2 \cos x = 0\) ; (ii) \(\sin x = 2.1 – 2\cos x\).
(d) From the graph, find y when x = 171°.
(a) A circle is inscribed in a square. If the sum of the perimeter of the square and the circumference of the circle is 100 cm, calculate the radius of the circle. [Take \(\pi = \frac{22}{7}\)].
(b) A rope 60cm long is made to form a rectangle. If the length is 4 times its breadth, calculate, correct to one decimal place, the :
(i) length ; (ii) diagonal of the rectangle.
(a) Using ruler and a pair of compasses only, construct : (i) quadrilateral PQRS such that /PQ/ = 10 cm, /QR/ = 8 cm, /PS/ = 6 cm, < PQR = 60° and < QPS = 75° ;
(ii) the locus \(l_{1}\) of points equidistant from QR and RS ; (iii) locus \(l_{2}\) of points equidistant from R and S ;
(b) Measure /RS/.
(a) Simplify \(\frac{x + 2}{x – 2} – \frac{x + 3}{x – 1}\)
(b) The graph of the equation \(y = Ax^{2} + Bx + C\) passes through the point (0, 0), (1, 4) and (2, 10). Find the :
(i) value of C ; (ii) values of A and B ; (iii) co-ordinates of the other point where the graph cuts the x- axis.
The marks scored by 50 students in a Geography examination are as follows :
60 54 40 67 53 73 37 55 62 43 44 69 39 32 45 58 48 67 39 51 46 59 40 52 61 48 23 60 59 47 65 58 74 47 40 59 68 51 50 50 71 51 26 36 38 70 46 40 51 42.
(a) Using class intervals 21 – 30, 31 – 40, …, prepare a frequency distribution table.
(b) Calculate the mean mark of the distribution.
(c) What percentage of the students scored more than 60%?
(a) A woman looking out from the window of a building at a height of 30m, observed that the angle of depression of the top of a flag pole was 44°. If the foot of the pole is 25m from the foot of the building and on the same horizontal ground, find, correct to the nearest whole number, the (i) angle of depression of the foot of the pole from the woman ; (ii) height of the flag pole.
(b)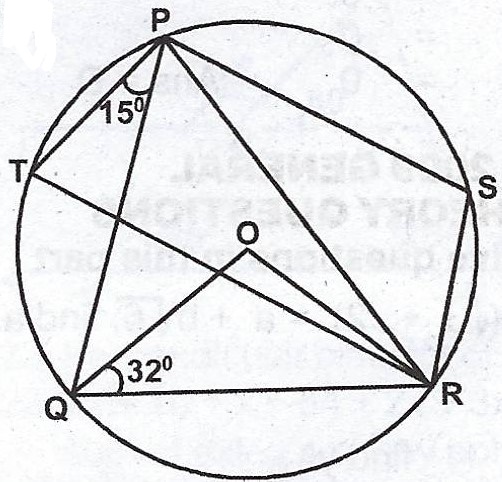 
In the diagram, O is the centre of the circle, < OQR = 32° and < TPQ = 15°. Calculate, (i) < QPR ; (ii) < TQo.
(a) If \(\log 5 = 0.6990, \log 7 = 0.8451\) and \(\log 8 = 0.9031\), evaluate \(\log (\frac{35 \times 49}{40 \div 56})\).
(b) For a musical show, x children were present. There were 60 more adults than children. An adult paid D5 and a child D2. If a total of D1280 was collected, calculate the
(i) value of x ; (ii) ratio of the number of children to the number of adults ; (iii) average amount paid per person ; (iv) percentage gain if the organisers spent D720 on the show.
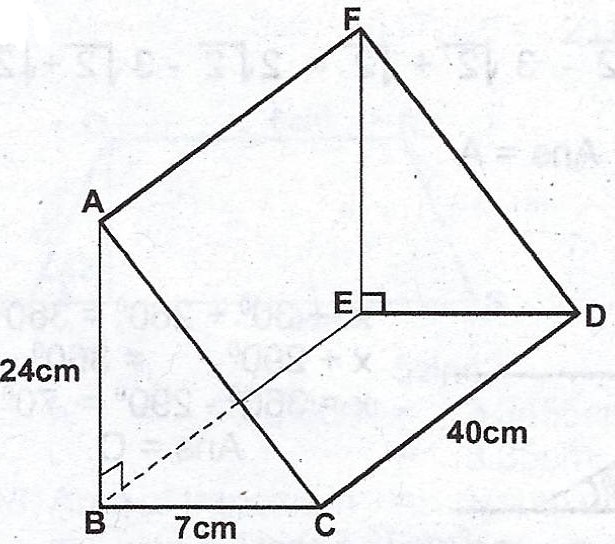
In the diagram, ABCDEF is a triangular prism. < ABC = < DEF = 90°, /AB/ = 24 cm, /BC/ = 7 cm and /CD/ = 40 cm. Calculate :
(a) /AC/ ;
(b) the total surface area of the prism.
(a) Out of 30 candidates applying for a post, 17 have degrees, 15 have diplomas and 4 neither degree nor diploma. How many of them have both?
(b) In triangle PQR, M and N are points on the side PQ and PR respectively such that MN is parallel to QR. If < PRQ = 75°, PN = QN and < PNQ = 125°, determine :
(i) < NQR ; (ii) < NPM.
The table shows the number of children per family in a community.
| No of children | 0 | 1 | 2 | 3 | 4 | 5 |
| No of families | 3 | 5 | 7 | 4 | 3 | 2 |
(a) Find the : (i) mode ; (ii) third quartile ; (iii) probability that a family has at least 2 children.
(b) If a pie chart were to be drawn for the data, what would be the sectorial angle representing families with one child?
(a) If \(9 \cos x – 7 = 1\) and \(0° \leq x \leq 90°\), find x.
(b) Given that x is an integer, find the three greatest values of x which satisfy the inequality \(7x < 2x – 13\).
(a) Given that \((\sqrt{3} – 5\sqrt{2})(\sqrt{3} + \sqrt{2}) = a + b\sqrt{6}\), find a and b.
(b) If \(\frac{2^{1 – y} \times 2^{y – 1}}{2^{y + 2}} = 8^{2 – 3y}\), find y.
(a) The third term of a Geometric Progression (G.P) is 24 and its seventh term is \(4\frac{20}{27}\). Find its first term.
(b) Given that y varies directly as x and inversely as the square of z. If y = 4, when x = 3 and z = 1, find y when x = 3 and z = 2.
The frequency distribution of the weight of 100 participants in a high jump competition is as shown below :
| Weight (kg) | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 | 60 – 69 | 70 – 79 |
|
Number of Participants |
10 | 18 | 22 | 25 | 16 | 9 |
(a) Construct the cumulative frequency table.
(b) Draw the cumulative frequency curve.
(c) From the curve, estimate the : (i) median ; (ii) semi- interquartile range ; (iii) probability that a participant chosen at random weighs at least 60 kg.
(a)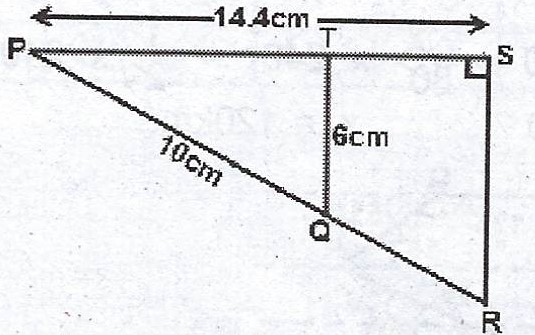 
In the diagram, < PTQ = < PSR = 90°, /PQ/ = 10 cm, /PS/ = 14.4 cm and /TQ/ = 6 cm. Calculate the area of the quadrilateral QRST.
(b) Two opposite sides of a square are each decreased by 10% while the other two are each increased by 15% to form a rectangle. Find the ratio of the area of the rectangle to that of the square.
(a) Copy and complete the table of values for the relation \(y = -x^{2} + x + 2; -3 \leq x \leq 3\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -4 | 2 | -4 |
(b) Using scales of 2 cm to 1 unit on the x- axis and 2 cm to 2 units on the y- axis, draw a graph of the relation \(y = -x^{2} + x + 2\).
(c) From the graph, find the : (i) minimum value of y ; (ii) roots of equation \(x^{2} – x – 2 = 0\) ; (iii) gradient of the curve at x = -0.5.
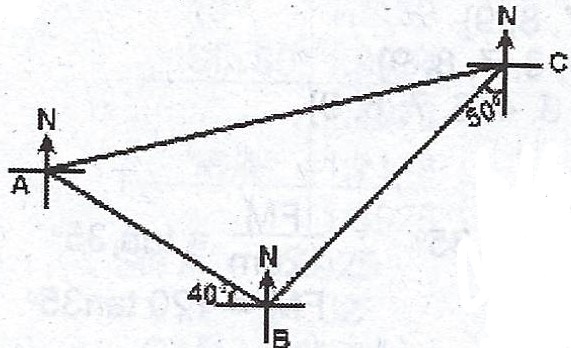In the diagram, /AB/ = 8 km, /BC/ = 13 km, the bearing of A from B is 310° and the bearing of B from C is 230°. Calculate, correct to 3 significant figures,
(a) the distance AC ;
(b) the bearing of C from A ;
(c) how far east of B, C is.
Using ruler and a pair of compasses only,
(a) construct (i) a quadrilateral PQRS with /PS/ = 6 cm, < RSP = 9 cm, /QR/ = 8.4 cm and /PQ/ = 5.4 cm; (ii) the bisectors of < RSP and < SPQ to meet at X ; (iii) the perpendicular XT to meet PS at T.
(b) Measure /XT/.
(a) Madam Kwakyewaa imported a quantity of frozen fish costing GH¢ 400.00. The goods attracted an import duty of 15% of its cost. She also paid a sales tax of 10% of the total cost of the goods including the import duty and then sold the goods for GH¢ 660.00. Calculate the percentage profit.
(b) In a school, there are 1000 boys and a number of girls. The 48% of the total number of students that were successful in an examination was made up of 50%of the boys and 40% of the girls. Find the number of girls in the school.
(a) The scale of a map is 1 : 20,000. Calculate the area, in square centimetres, on the map of a forest reserve which covers 85\(km^{2}\).
(b) A rectangular playing field is 18m wide. It is surrounded by a path 6m wide such that its area is equal to the perimeter of the path. Calculate the length of the field.
(c)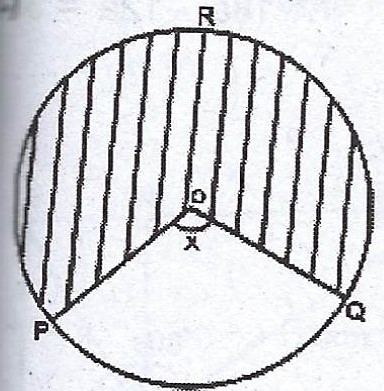 
The diagram shows a circle centre O. If < POQ = x°, the diameter of the circle is 7 cm and the area of the shaded portion is 27.5\(cm^{2}\). Find, correct to the nearest degree, the value of x. [Take \(\pi = \frac{22}{7}\)].