|
Class Interval |
Frequency |
| 60 – 64 | 2 |
| 65 – 69 | 3 |
| 70 – 74 | 6 |
| 75 – 79 | 11 |
| 80 – 84 | 8 |
| 85 – 89 | 7 |
| 90 – 94 | 2 |
| 95 – 99 | 1 |
The table shows the distribution of marks scored by students in an examination. Calculate, correct to 2 decimal places, the
(a) mean ; (b) standard deviation of the distribution.
Three towns X, Y and Z are such that Y is 20 km from X and 22 km from Z. Town X is 18 km from Z. A health centre is to be built by the government to serve the three towns. The centre is to be located such that patients from X and Y travel equal distance to access the health centre while patients from Z will travel exactly 10 km to reach the Health centre.
(a) Using a scale of 1 cm to 2 km, find the construction, using a pair of compasses and ruler only, the possible positions the Health centre can be located.
(b) In how many possible locations can the Health centre be built?
(c) Measure and record the distances of the location from town X.
(d) Which of these locations would be convenient for all three towns?
A point H is 20 m away from the foot of a tower on the same horizontal ground. From the point H, the angle of elevation of the point P on the tower and the top (T) of the tower are 30° and 50° respectively. Calculate, correct to 3 significant figures :
(a) /PT/; (b) the distance between H and the top of the tower
(c) The position of H if the angle of depression of H from the top of the tower is to be 40°.
(a) (i) Using a scale of 2 cm to 1 unit on both axes, on the same graph sheet, draw the graphs of \(y – \frac{3x}{4} = 3\) and \(y + 2x = 6\).
(ii) From your graph, find the coordinates of the point of intersection of the two graphs.
(iii) Show, on the graph sheet, the region satisfied by the inequality \(y – \frac{3}{4}x \geq 3\).
(b) Given that \(x^{2} + bx + 18\) is factorized as \((x + 2)(x + c)\). Find the values of c and b.
(a) A boy had M Dalasis (D). He spent D15 and shared the remainder equally with his sister. If the sister’s share was equal to \(\frac{1}{3}\) of M, find the value of M.
(b) A number of tourists were interviewed on their choice of means of travel. Two- thirds said that they travelled by road, \(\frac{13}{30}\) by air and \(\frac{4}{15}\) by both air and road. If 20 tourists did not travel by either air or road ; (i) represent the information on a Venn diagram ; (ii) how many tourists (1) were interviewed ; (2) travelled by air only?
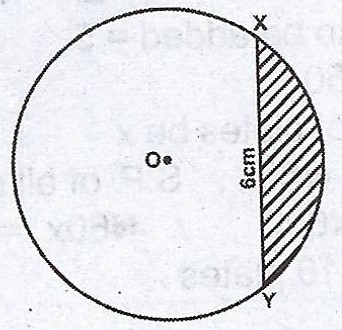
In the diagram, O is the centre of the circleand XY is a chord. If the radius is 5 cm and /XY/ = 6 cm, calculate, correct to 2 decimal places, the :
(a) angle which XY subtends at the centre O ;
(b) area of the shaded portion.
(a) A box contains 40 identical discs which are either red or white. If the probability of picking a red disc is \(\frac{1}{4}\); Calculate the number of (i) white discs ; (ii) red discs that should be added such that the probability of picking a red disc will be \(\frac{1}{3}\).
(b) A salesman bought some plates at N50.00 each. If he sold all of them for N600.00 and made a profit of 20% on the transaction, how many plates did he buy?
(a) 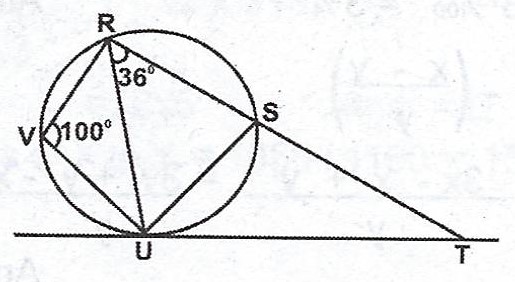 In the diagram, TU is tangent to the circle. < RVU = 100° and < URS = 36°. Calculate the value of angle STU.
In the diagram, TU is tangent to the circle. < RVU = 100° and < URS = 36°. Calculate the value of angle STU.
(b) In triangle XYZ, |XY| = 5 cm, |YZ| = 8 cm and |XZ| = 6 cm. P is a point on the side XY such that |XP| = 2 cm and the line through P, parallel to YZ meets XZ at Q. Calculate |QZ|.
Sonny is twice as old as Wale. Four years ago, he was four times as old as Wale. When will the sum of their ages be 66?
(a) Simplify : \(\frac{1\frac{1}{4} + \frac{7}{9}}{1\frac{4}{9} – 2\frac{2}{3} \times \frac{9}{64}}\)
(b) Given that \(\sin x = \frac{2}{3}\), evaluate, leaving your answer in surd form and without using tables or calculator, \(\tan x – \cos x\).
When one end of a ladder, LM, is placed against a vertical wall at a point 5 metres above the ground, the ladder makes an angle of 37° with the horizontal ground.
(a) Represent this information in a diagram ;
(b) Calculate, correct to 3 significant figures, the length of the ladder ;
(c) If the foot of the ladder is pushed towards the wall by 2 metres, calculate,correct to the nearest degree, the angle which the ladder nows makes with the ground.
An aeroplane flies due North from a town T on the equator at a speed of 950km per hour for 4 hours to another town P. It then flies eastwards to town Q on longitude 65°E. If the longitude of T is 15°E,
(a) represent this information in a diagram ;
(b) calculate the : (i) latitude of P, correct to the nearest degree ; (ii) distance between P and Q, correct to four significant figures. [Take \(\pi = \frac{22}{7}\); Radius of the earth = 6400km].
The frequency distribution table shows the marks obtained by 100 students in a Mathematics test.
|
Marks (%) |
1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
| Frequency | 2 | 3 | 5 | 13 | 19 | 31 | 13 | 9 | 4 | 1 |
(a) Draw the cumulative curve for the distribution.
(b) Use the graph to find the : (i) 60th percentile ; (ii) probability that a student passed the test if the pass mark was fixed at 35%.
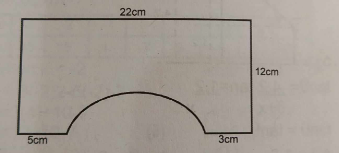
(a)
A segment of a circle is cut off from a rectangular board as shown in the diagram. If the radius of the circle is \(1\frac{1}{2}\) times the length of the chord; calculate, correct to 2 decimal places, the perimeter of the remaining portion. [Take \(\pi = \frac{22}{7}\)]
(b) Evaluate without using calculators or tables, \(\frac{3}{\sqrt{3}}(\frac{2}{\sqrt{3}} – \frac{\sqrt{12}}{6})\).
(a) Using ruler and a pair of compasses only, construct : (i) a trapezium WXYZ such that |WX| = 10.2 cm, |XY| = 5.6 cm, |YZ| = 5.8 cm, < WXY = 60° and WX is parallel to YZ (ii) a perpendicular from Z to meet \(\overline{WX}\) at N.
(b) Measure : (i) |WZ| ; (ii) |ZN| .
(a) If (3 – x), 6, (7 – 5x) are consecutive terms of a geometric progression (GP) with constant ratio r > 0, find the :
(i) values of x ; (ii) constant ratio.
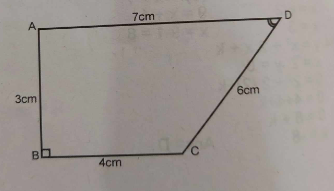
(b) In the diagram above, |AB| = 3 cm, |BC| = 4 cm, |CD| = 6 cm and |DA| = 7 cm. Calculate
(a) Copy and complete the table of values for the relation \(y = 3x^{2} – 5x – 7\).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 35 | -7 | -9 | 5 |
(b) Using scales of 2 cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of \(y = 3x^{2} – 5x – 7, -3 \leq x \leq 4\).
(c) From the graph : (i) find the roots of the equation \(3x^{2} – 5x – 7 = 0\) ; (ii) estimate the minimum value of y ; (iii) calculate the gradient of the curve at the point x = 2.
(a) Two positive whole numbers p and q are such that p is greater than q and their sum is equal to three times their difference;
(i) Express p in terms of q ; (ii) Hence, evaluate \(\frac{p^{2} + q^{2}}{pq}\).
(b) A man sold 100 articles at 25 for N66.00 and made a gain of 32%. Calculate his gain or loss percent if he sold them at 20 for N50.00.
A boy 1.2m tall, stands 6m away from the foot of a vertical lamp pole 4.2m long. If the lamp is at the tip of the pole,
(a) represent this information in a diagram ;
(b) calculate the (i) length of the shadow of the boy cast by the lamp ; (ii) angle of elevation of the lamp from the boy, correct to the nearest degree.
The area of a circle is \(154cm^{2}\). It is divided into three sectors such that two of the sectors are equal in size and the third sector is three times the size of the other two put together. Calculate the perimeter of the third sector. [Take \(\pi = \frac{22}{7}\)].
(a) The present ages of a father and his son are in the ratio 10 : 3. If the son is 15 years old now, in how many years will the ratio of their ages be 2 : 1?
(b) The arithmetic mean of x, y and z is 6 while that of x, y, z, l, u, v and w is 9. Calculate the arithmetic mean of l, u, v and w.

